Quarter Million Year Canon
of Solar System Transits
by John Walker
In astronomy, a planetary transit is when a planet closer to the Sun passes in front of the Sun's disc as seen from a more distant planet. From the Earth, transits of Mercury and Venus are visible; recently, observers were treated to these spectacles in back-to-back years: 2003 and 2004.
In the run-up to the 2004 transit of Venus, I became obsessed with one of those silly questions which, once they sink their claws into one's mind, won't go away without being answered yes or no. Is there ever a simultaneous transit of Mercury and Venus visible from the Earth?
| A glossary of technical terms used in this document appears at the end. |
The naïve answer is, “Of course not (you idiot)! Transits can occur only when inferior conjunction with the inner planet coincides with its crossing the ecliptic. Transits of Venus always occur in June and December, transits of Mercury in May and November, and thus a simultaneous transit can never happen.”
But this doesn't take into account the evolution of planetary orbits over time. Analytical planetary theories such as VSOP87 are useless beyond the period for which they are fit (say, −4000 to +8000 years Gregorian). To go beyond that, you need to do full-up numerical integration of the motion of the Sun and planets.
Well, that's what computers are for, isn't it? So, I found a
high-precision numerical integration code for the Solar System
written by Steve Moshier,
built a back-end to search for transits, and set it looking for
this extraordinarily rare event. Since I didn't want to burn
months of computing time with nothing to show for it, I
decided to prepare a canon of all Solar System transits
(excluding marginal graze events) visible in the time interval I
chose, namely a quarter million years centred on the start of
the so-called “Common Era”. Here it is.
The Great Race
What I didn't know when I undertook this quest was that I had inadvertently entered a race with Jean Meeus, the Cosmic Grand Master of computational positional astronomy. This question had also occurred to him, and he started earlier, collaborated with numerical integration expert Aldo Vitagliano, found the answer before I did, and published it in the June 2004 issue of The Journal of the British Astronomical Association while I was still computing. When it comes to number crunching astronomical data, getting into a race with Jean Meeus is like challenging Michael Schumacher to five laps, he in his Ferrari, you in your Volkswagen bus. I was beaten, fair and square: congratulations, Jean: this discovery is a tremendous achievement, and I'm happy to play harmony on my smallest second fiddle in confirming it with an independent investigation (although we may have used common integration code and/or initial state vectors).
…and the Answer Is…

Click image to play movie of this event.
Yes, there is, or rather will be, a simultaneous transit of Mercury and Venus visible from the Earth. It will happen in the year 69163, on the 26th of July (assuming the calendar hasn't been changed to re-synchronise trivialities like the Earth's rotation and orbit with grander matters such as the planets in their orbits, which is not the way to bet—astronomers will prefer to identify this as the event of Julian day 26982533 [barycentric dynamical time].)
I've made a movie of this event. Venus is the large white sphere which appears first, Mercury the fleeting green messenger zipping in for its own rapid transit; they aren't both simultaneously in transit for long, but it's unambiguous, and only happens once in the quarter million years I searched for such events. (Of course, both of these planets would appear as perfectly black dots against the disc of the Sun. I've taken the liberty of colour coding them so you can see them approach the limb of the Sun in the movie, and also to help tiny Mercury show up better in an image at this scale.)
Transit Index Table
The following table gives the number of transits of objects in the column headings as seen from bodies in the row titles. Clicking on column headings displays a list of all transits of that body visible from outer planets. Clicking on a row title shows all transits visible from that planet. Clicking a cell within the table lists the transits of the body in the column seen from that in the row. Some of these transit catalogue files are large; the quarter million year canon includes a total of 487,407 transits of Mercury alone! To minimise download time, these files are compressed with Gzip. Most modern browsers automatically uncompress such files and display them like any other Web page. If your browser insists on saving the file to disc, go ahead and do so, then uncompress it with Gzip and view the resulting HTML with a “file:” URL. If you don't understand what this means, I can't help you.
| From / Of | Mercury | Venus | Earth | Moon | Mars | Jupiter | Saturn | Uranus | Neptune | Total from |
|---|---|---|---|---|---|---|---|---|---|---|
| Venus | 30165 | 30165 | ||||||||
| Earth | 40540 | 2964 | 43504 | |||||||
| Moon | 40443 | 2984 | 43427 | |||||||
| Mars | 54411 | 13099 | 3392 | 3399 | 74301 | |||||
| Jupiter | 68795 | 49274 | 23635 | 23635 | 4962 | 170301 | ||||
| Saturn | 73583 | 55349 | 28373 | 28360 | 8607 | 160 | 194432 | |||
| Uranus | 73928 | 55766 | 29404 | 29380 | 7818 | 461 | 67 | 196824 | ||
| Neptune | 76531 | 63576 | 33187 | 33172 | 10702 | 754 | 125 | 2 | 218049 | |
| Pluto | 29011 | 5744 | 2555 | 2550 | 883 | 38 | 9 | 40790 | ||
| Total of | 487407 | 248756 | 120546 | 120496 | 32972 | 1413 | 201 | 2 | 1011793 |
The numbers in the rightmost column are the total number of transits of all planets visible from the planet in the row, and the numbers in the bottom row are the total number of transits of the planet in the column visible from all other planets. The number at the bottom right is the total number of transits in the canon: 1,011,793. There are thus about 4 transits of one planet by another every year. The entries for “transits” involving the Earth and Moon are vacant; such events are known as solar and lunar eclipses, and require more complicated computations than ordinary planetary transits—they were ignored in this project.
Download Complete Canon Database
You can download the entire quarter million year canon of transits in Comma Separated Value (CSV) format from the download centre at the end of this document. The canon database consists of the file transits.csv, which contains records describing all solar system transits in the years ±125,000, sorted in ascending order by the start time of the transit. Fields in the records are as follows.
- Transit of. Name of the planet (e.g. “Venus”, “Mars”) transiting the Sun.
- Visible from. Name of the planet from which the transit is visible.
- First. Julian day number of integration step when transit first observed.
- Maximum. Julian day number of integration step when transit reached maximum magnitude (planet closest to apparent centre of the solar disc).
- Last. Julian day number of integration step when transit last observed.
- Solar radius. Mean radius of the Sun as seen from the “Visible from” planet in degrees.
- Depth. Angular distance, in degrees, of the centre of the “Transit of” planet from the apparent centre of the solar disc at the “Maximum” time. A perfectly central transit would have a “Depth” of zero, while a graze will have a “Depth” comparable to the “Solar Radius”.
For example, here is the record from the canon for the 2004 Transit of Venus:
Venus,Earth,2453164.73,2453164.84,2453164.96,.2626,.1736
This denotes a transit of Venus visible from the Earth, first observed at 5:31 UTC on 2004-06-08 (use our Calendar Converter to convert Julian day numbers to your calendar of choice), with maximum transit observed at 8:09 UTC that day when Venus was 0.1736° from the centre of the solar disc which subtended a radius of 0.2626° from the Earth, with Venus last observed in transit at 11:02 UTC.
There's an important reason for all the verbiage about “integration steps” and “observed” in the discussion above. The canon was created by evolving the solar system forward and backward by stepwise numerical integration. The step size used in the integration was 1/100 of day, or a little less than 15 minutes. This is sufficiently small for the integration to be well behaved numerically and not to miss significant transit events, while large enough that the integration finishes before everybody dies off or forgets why we were running it in the first place. Every event in the canon occurs at a multiple of this integration step size! It is thus incorrect to speak of a transit “beginning” at the First time or ending at the Last time, as the actual duration of the transit will always be longer than the time between the first and last integration steps when it was observed in progress. Likewise, the Maximum time and Depth at that time are the integration step at which the planet most closely approached the centre of the Sun's apparent disc, not the actual moment of closest approach.
The finite granularity of the integration also means that near-grazing transits whose entire duration is less than one integration step will be reported only if an integration step happens to fall within their duration. Further, a planet is considered in transit only if its centre is equal to or less than the mean apparent solar radius as seen by an observer at the centre of the Visible from planet. Hence, extreme grazes (which may be visible only from a portion of the outer planet's surface) do not figure in the canon.
Multiple Transits

|
| Simultaneous transit of Venus, Earth, and the Moon seen from Saturn, JD 10254935.97, 23364-12-16. While this “triple transit” is in progress from Saturn, Venus transits the Sun as seen from both the Earth and Moon. Thus, there are five transits in progress at one time. |
| Multiple Transits | Visible From |
|---|---|
| 1 | Earth |
| 1 | Moon |
| 8 | Mars |
| 12 | Pluto |
| 69 | Jupiter |
| 108 | Saturn |
| 108 | Uranus |
| 145 | Neptune |
Multiple transits—simultaneous transits of two or more planets visible from a third, are among the rarest of Solar System mutual events. Here is a table of the frequency of such events in the canon in decreasing order of rarity. We don't consider a transit of the Earth and Moon seen from another planet as a multiple transit since they're so common, but we do distinguish “triple transits” involving the Earth, Moon, and another planet from those of just the Earth or Moon and another planet.
There are a total of 452 multiple transits (two planets, including the Earth's Moon as a planet, but excluding transits of just the Earth and Moon) in the quarter million year canon. The table at the right gives the number of multiple transits visible from each planet. The single event visible from the Earth and Moon is what I was looking for when I began this project—the simultaneous transit of Mercury and Venus of July 69163.
| Triple Transits | Visible From |
|---|---|
| 1 | Mars |
| 4 | Pluto |
| 10 | Jupiter |
| 23 | Uranus |
| 26 | Saturn |
| 30 | Neptune |
As you might expect from the general transit table, Neptune is the big winner again; the combination of having 8 candidate inner planets (counting the Moon) and an orbit nearly coplanar with the ecliptic gives it the edge. Still, note that a total of 145 events in 250,000 years means you'll have to wait, on average, more than 1700 years between multiple transits, even from the best planetary vantage point in the Solar System.
A total of 94 of these multiple transits are “triple transits” in which both the Earth and Moon are in transit simultaneously along with another planet. The triple transit visible from Mars is a transit of the Earth, Moon, and Mercury which occurred in the year −55962 (Julian calendar) so, sadly, you missed it, and no other triple transit from Mars figures in the canon.
The following table gives frequencies of all the multiple transit events in the canon, by viewpoint and the bodies in transit. As you can see, simultaneous transits of Mercury and Venus are by far the most common—it's just that you have to go to the outer planets to see more than a handful in a quarter million years.
For details of specific events, see the complete
Catalogue
of Simultaneous Transits.
| Occurrences | From | Transit Of | Occurrences | From | Transit Of | |
|---|---|---|---|---|---|---|
| 1 | Earth | Mercury Venus | 6 | Jupiter | Mercury Mars | |
| 1 | Moon | Mercury Venus | 6 | Jupiter | Venus Moon | |
| 1 | Mars | Mercury Moon | 6 | Uranus | Mercury Mars | |
| 1 | Mars | Mercury Earth Moon | 7 | Jupiter | Venus Earth | |
| 1 | Saturn | Mercury Mars | 7 | Saturn | Venus Earth Moon | |
| 1 | Pluto | Venus Earth | 7 | Saturn | Venus Moon | |
| 1 | Pluto | Venus Moon | 8 | Jupiter | Mercury Earth | |
| 1 | Pluto | Venus Earth Moon | 8 | Neptune | Mercury Mars | |
| 1 | Pluto | Earth Moon Mars | 9 | Uranus | Venus Earth Moon | |
| 1 | Pluto | Earth Mars | 10 | Saturn | Venus Earth | |
| 1 | Pluto | Moon Mars | 10 | Uranus | Venus Moon | |
| 2 | Mars | Mercury Earth | 10 | Uranus | Venus Earth | |
| 2 | Jupiter | Venus Mars | 13 | Neptune | Mercury Earth Moon | |
| 2 | Neptune | Venus Jupiter | 14 | Uranus | Mercury Earth Moon | |
| 2 | Neptune | Earth Mars | 15 | Neptune | Mercury Moon | |
| 2 | Neptune | Earth Moon Mars | 15 | Neptune | Venus Earth Moon | |
| 2 | Neptune | Moon Mars | 16 | Saturn | Mercury Earth Moon | |
| 2 | Pluto | Mercury Moon | 16 | Saturn | Mercury Moon | |
| 2 | Pluto | Mercury Earth Moon | 16 | Uranus | Mercury Earth | |
| 2 | Pluto | Mercury Earth | 16 | Uranus | Mercury Moon | |
| 3 | Saturn | Earth Moon Mars | 18 | Saturn | Mercury Earth | |
| 3 | Saturn | Earth Mars | 18 | Neptune | Mercury Earth | |
| 3 | Saturn | Moon Mars | 18 | Neptune | Venus Moon | |
| 3 | Neptune | Mercury Jupiter | 19 | Neptune | Venus Earth | |
| 4 | Mars | Mercury Venus | 24 | Jupiter | Mercury Venus | |
| 5 | Jupiter | Mercury Earth Moon | 24 | Saturn | Mercury Venus | |
| 5 | Jupiter | Venus Earth Moon | 27 | Uranus | Mercury Venus | |
| 6 | Jupiter | Mercury Moon | 28 | Neptune | Mercury Venus |
A database of all multiple events in CSV format may be downloaded. Records in this database have the following format:
1. From. Name of the planet (e.g. “Venus”, “Mars”) from which the multiple transit is visible. 2. Mult_First. Julian day number when multiple transit first observed. 3. Mult_Last. Julian day number when multiple transit last observed. 4. nBodies. Number of bodies in transit simultaneously between Mult_First and Mult_Last.
Following these fields are nBodies groups of four fields each containing the following information for each body n (1, 2,…) in the multiple transit.
4n+1. Name_n. Name of transiting body. 4n+2. First_n. Julian day number of integration step when transit of body n first observed. 4n+3. Maximum_n. Julian day number of integration step when transit of body n reached maximum magnitude (planet closest to apparent centre of the solar disc). 4n+4. Last_n. Julian day number of integration step when transit of body n last observed.
The duration of the multiple transit will be always be shorter than those of the individual bodies involved. In the case of a triple transit involving the Earth, Moon, and a third planet, the database will contain separate records for the double transits of Earth and the planet, the Moon and the planet, and the triple event when Earth, Moon, and the planet were all in transit together. Since double transits involving just the Earth and Moon are excluded, there will be no record for such an event even if it occurs in conjunction with an eligible multiple transit.
There are no events in the canon in which three main planets (excluding the Moon) are simultaneously in transit from an outer planet. Does this ever happen? Consider it a challenge!
The Orbit of the Sun
| Radii | Julian Day | Date | Time | Cal |
|---|---|---|---|---|
| Barycentre Minima | ||||
| 0.001 | -10390616.60 | -33161-01-16 | 21:35 | J |
| 0.002 | -43762733.70 | -124529-03-01 | 19:13 | J |
| 0.002 | -5073521.61 | -18604-06-15 | 21:21 | J |
| 0.002 | 46534475.09 | 122694-12-18 | 14:07 | G |
| 0.003 | -27240190.45 | -79293-06-04 | 01:11 | J |
| 0.003 | -22982280.50 | -67636-12-11 | 23:59 | J |
| 0.003 | -13588979.22 | -41918-05-28 | 06:42 | J |
| 0.003 | -11637617.67 | -36576-12-09 | 19:54 | J |
| 0.003 | 12023089.66 | 28206-01-01 | 03:50 | G |
| 0.003 | 14721699.96 | 35594-07-18 | 11:02 | G |
| Barycentre Maxima | ||||
| 2.224 | -18213155.43 | -54578-02-06 | 01:40 | J |
| 2.224 | 31821151.92 | 82411-04-03 | 10:05 | G |
| 2.225 | 2198229.94 | 1306-06-05 | 10:33 | J |
| 2.225 | 22427794.24 | 56693-02-10 | 17:46 | G |
| 2.225 | 36825871.82 | 96113-09-17 | 07:40 | G |
| 2.226 | 508185.88 | -3322-05-04 | 09:07 | J |
| 2.227 | 31755789.21 | 82232-04-18 | 17:03 | G |
| 2.228 | -19903214.10 | -59206-12-21 | 09:35 | J |
| 2.235 | 35135860.85 | 91486-08-14 | 08:24 | G |
| 2.236 | 33445833.24 | 86859-06-24 | 17:46 | G |
Numerical integration of the Solar System is performed in a co-ordinate system with the origin at the barycentre of the Solar System, as opposed to the centre of the Sun. This is because one has to account for the orbit of the Sun. “Orbit of the Sun?”, you exclaim. “Well certainly the Sun has its orbit around the Galaxy, but don't the planets just orbit the Sun like you always see in an orrery?” No, not even close.
The barycentre of a set of masses is their instantaneous centre of mass. (The definition gets more complicated when you account for relativity, but we can neglect that for the purposes of this discussion.) Although the Sun is by far the most massive object in the Solar System, the gas giant planets, Jupiter and Saturn in particular, are far from negligible: Jupiter is 1/1047 the mass of the Sun and Saturn 1/3499, and both are far enough away to have a substantial lever effect against the Sun's mass.
While searching for transits, I also kept track of minimal and maximal distances of the Solar System barycentre from the centre of the Sun, and the moments at which the barycentre exited and re-entered the Sun, taking 696,000 kilometres as the mean solar radius. Examining the period in the canon between the first and last passages of the barycentre through the surface of the Sun, we find that in a total of 91,305,716 days (about 249,987 present-day mean solar years), the barycentre of the Solar system was outside the Sun a total of 58,888,175 days, or 64.5% of the time, and inside for 32,417,541 days, 35.5% of the total.
The Sun, then, not only has an orbit within the Solar System, almost
two thirds of the time the point it's orbiting about is outside
the Sun! This makes one wonder just how far the barycentre ever
gets from the centre of the Sun. I also kept track of minimum and
maximum barycentre distances (both local and global—whenever the
sign of the first derivative of the barycentre distance changes).
The table at the right shows the ten closest approaches of the
barycentre to the centre of the Sun and the ten most distant
excursions, in units of mean solar radii. At the all-time maximum for
the period of the integration in the year 86859, the barycentre will
be 2.236 solar radii from the centre of the Sun. In other words, if
you focused on the barycentre and watched the Sun in its orbit, it
would be swinging around a point 1.236 solar radii outside the Sun.
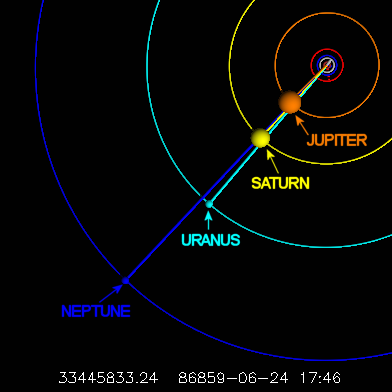 Extreme barycentre maxima occur at moments of close
alignment of the massive outer planets. At the left is an
orrery rendering of the June 86859 event.
The sizes of the planets have been inflated by a factor of 2500 to
make them visible on the scale of the Solar System, and their orbits
have been plotted along with vectors from the Solar System barycentre
to each planet. You can't see much of the inner system at this
scale, but the lightweight terrestrial planets (and Pluto) are
essentially irrelevant against these heavy hitters. Below, to the
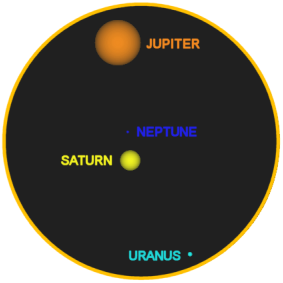
right, is a simulated binocular view of this planetary conjunction.
The circle represents a 6° field of view, typical of 10 power
binoculars. I've blown up the size of the planets in this image by a
factor of 100—in real binoculars, Uranus and Neptune would be dim
dots and the discs of Jupiter and Saturn barely perceptible. Oh yes,
and Saturn's rings are missing here. The separation between Jupiter
and Uranus is 4.94°, so the whole conjunction fits within a five
degree circle—that's about the diameter of ten full Moons, and
smaller than the bowl of the Big Dipper.
Extreme barycentre maxima occur at moments of close
alignment of the massive outer planets. At the left is an
orrery rendering of the June 86859 event.
The sizes of the planets have been inflated by a factor of 2500 to
make them visible on the scale of the Solar System, and their orbits
have been plotted along with vectors from the Solar System barycentre
to each planet. You can't see much of the inner system at this
scale, but the lightweight terrestrial planets (and Pluto) are
essentially irrelevant against these heavy hitters. Below, to the
right, is a simulated binocular view of this planetary conjunction.
The circle represents a 6° field of view, typical of 10 power
binoculars. I've blown up the size of the planets in this image by a
factor of 100—in real binoculars, Uranus and Neptune would be dim
dots and the discs of Jupiter and Saturn barely perceptible. Oh yes,
and Saturn's rings are missing here. The separation between Jupiter
and Uranus is 4.94°, so the whole conjunction fits within a five
degree circle—that's about the diameter of ten full Moons, and
smaller than the bowl of the Big Dipper.
 Because the barycentre location is influenced by the positions of all
the planets, it doesn't evolve in any kind of regular manner—it can
loop smoothly from inside the Sun to outside and back, or it can
“wiggle” through a number of local minima and maxima while inside or
outside the Sun. On two occasions within the period of the canon, in
the years 47371–47387 and 96880–96895, the barycentre makes a total
of 13 minima and maxima between the time it exits the Sun and when it
re-enters. There's more room to roam outside the Sun than inside,
and the greatest number of minima and maxima between the barycentre's
entering the Sun and departing it is 9, which occurs six times within
the canon. All of the data used in these analyses and everything you
need to answer a multitude of other curious questions, all utterly
devoid of scientific import, may be found in the
barycentre database archive
available from the download centre.
Because the barycentre location is influenced by the positions of all
the planets, it doesn't evolve in any kind of regular manner—it can
loop smoothly from inside the Sun to outside and back, or it can
“wiggle” through a number of local minima and maxima while inside or
outside the Sun. On two occasions within the period of the canon, in
the years 47371–47387 and 96880–96895, the barycentre makes a total
of 13 minima and maxima between the time it exits the Sun and when it
re-enters. There's more room to roam outside the Sun than inside,
and the greatest number of minima and maxima between the barycentre's
entering the Sun and departing it is 9, which occurs six times within
the canon. All of the data used in these analyses and everything you
need to answer a multitude of other curious questions, all utterly
devoid of scientific import, may be found in the
barycentre database archive
available from the download centre.
Dates and Reasons
Using any kind of calendar date for events in the distant past and future is highly problematic. Even in the historical era, different calendars have been used at various times and places. For example, the Gregorian calendar was proclaimed in 1582, but not adopted in Great Britain and its colonies until 1752. Historians studying documents dating between those years must be careful not to confuse Julian dates in British texts with Gregorian dates used on the continent. See our Calendar Converter for a small sample of calendars used in the past and present.
To avoid these ambiguities, and to facilitate doing arithmetic with dates (for example, subtracting the dates of eclipses of a double star to determine its orbital period), astronomers use Julian day numbers, which are simply the number of days and fraction of a day elapsed since noon at the Greenwich meridian on Monday, January 1st of year 4713 BCE in the Julian calendar. All recorded historical astronomical observations date from after that epoch and consequently bear positive Julian day numbers.
Julian day numbers were used exclusively in all of the calculations upon which this document was based, and are the definitive dates in the databases associated herewith. However, even though it's easy to convert Julian days to other calendars, most people find it hard to get an intuitive feel for the relationship of a date like “26982533.31” with the present. To make the results from this computation more accessible and only for that purpose, I have expressed Julian day numbers as civil dates in the Gregorian calendar for dates starting with Julian day 2299160.5 (October 15th, 1582 in the Gregorian calendar), and in the Julian calendar for prior dates. Astronomers often use this convention when discussing historical observations, while being careful not to be confused, for example, by reports of eclipse observations from England in Newton's time.
Arbitrarily extending these calendars forward and backward over a hundred-plus millennia is a highly dubious endeavour, but what are you going do? It's a choice of just using Julian days exclusively, which people don't understand (or will blindly convert into civil dates anyway, without thinking of the implications), or showing civil dates as a rough guideline, not to be taken literally, as to when events occur.
Civil calendars were never intended to be used across such long spans of time. The Julian calendar (the calendar used from Roman times until 1582 [or whenever], as opposed to Julian day numbers) loses a day with respect to the seasons every 128 years. The Gregorian calendar, with its more complicated leap year rule, is a tremendous improvement over the Julian, and only slips one day about every 3300 years. But if we're looking out 125,000 years into the future, that's a cumulative error of almost 38 days—more than a month.
But while the calendar is slipping, the seasons themselves are slipping even faster. The Earth's axis of rotation precesses with respect to the fixed stars, which causes the date of the vernal equinox—the start of spring in the northern hemisphere and fall in the southern, to shift through the year with a period of about 26,000 years. When we look 125,000 years into the future or past, that's almost five complete precession cycles, which completely invalidates the relationship between any civil calendar and the seasons.
It gets worse. Solar calendars are based upon days and years, and assume the relationship between these two time intervals remains fixed. But it doesn't—tidal friction, largely due to ocean tides acting against shorelines, inexorably causes the length of the day to increase and the Moon to recede from the Earth, eventually putting an end to total solar eclipses. Ever since 1972, leap seconds have been periodically added to precise official measures of time to prevent them from slipping out of synchronism with the actual rotation of the Earth. Over the short term many things, not entirely understood, affect the Earth's rotation, but on the average over the last three decades, about one leap second has been added per year. If this rate continues over the centuries, the discrepancy between time measured with respect to the Earth's rotation and Solar System and other astronomical events independent of it (which, of course, include planetary motion and hence transits) will add up, after 125,000 years in the future, to about 35 hours, or almost a day and half. And that assumes the rate of change in the Earth's rotation remains constant—an ice age or melting of the polar caps would substantially change the tidal braking rate, and you'll recall there have been two ice ages in the past 125,000 years. If the Earth's rotation does continue to slow at the rate it has for the last two centuries, after 125 centuries each day will be about 1.4 seconds longer, and timekeeping will doubtless have been adjusted to compensate, requiring changes in calendars as well.
Transits are reported in barycentric dynamical time when bodies align such that an inner planet is geometrically in front of the Sun as seen from the outer planet. But since the speed of light is finite (it takes almost exactly 500 seconds for light to travel one astronomical unit, a handy factoid to memorise and impress your friends), so when, for example, in the frame of reference of the Solar System barycentre the Sun, Mercury, and Neptune line up to produce a transit of Mercury, photons showing the event in progress will not arrive at Neptune, which orbits at around 30 astronomical units from the Sun, for 30×500=15000 seconds, or about four hours later. An astronomer at Neptune with a clock synchronised to barycentric dynamical time would observe the apparent start of the transit more than four hours after the geometric alignment which produced it occurred in the barycentric reference frame.
And that's just the simple stuff! Due to special and general relativity, the rate at which a clock runs depends upon its motion relative to an observer and the ambient gravitational field. Clocks on the surface of the Earth are not only in a gravitational field, but are constantly in motion with respect to other Solar System bodies as the Earth rotates and orbits the Sun. These effects could be neglected in the days of mechanical clocks, but are sufficiently large that the Global Positioning System (GPS) would not provide usable accuracy were the clocks in the satellites not corrected for these effects (less technical discussion).
Timekeeping on the Earth, measured in days (the Earth's rotation) and years (the Earth's orbit around the Sun), has nothing whatsoever to do with the Solar System in the large. When evolving the Solar System backward or forward in time, we use a system of time called “Barycentric Coordinate Time”, abbreviated TCB, in units of “days”, where a day is 86,400 seconds as defined physically by the SI system of units, as would be measured by an atomic clock at the location of the Solar System barycentre, but unperturbed by the gravitational field of the Sun and other solar system bodies. (Obviously, since the barycentre of the Solar System is inside the Sun about a third of the time, this is a theoretical notion.) The hypothetical TCB clock keeps time regardless of motion in the Solar System, and provides a uniform time scale for calculating its evolution. Over the near term, the discrepancies between this idealised clock and concepts of time and date socially constructed by talking apes out on the third planet can be neglected, but any mention of “the transit of Mercury, Earth, and Moon visible from Uranus on the afternoon of Friday, May 24th, A.D. 124097, London time” should be taken not cum grano salis but cum dolio salis.
The Big Crunch
The orbit of any one planet depends on the combined motion of all the planets, not to mention the action of all of these on each other. But to consider simultaneously all these causes of motion and to define these motions by exact laws allowing of conventional calculation exceeds, unless I am mistaken, the force of the entire human intellect.Isaac Newton, Philosophiæ Naturalis Principia Mathematica
Perhaps there's never been a human intellect the equal of Newton's,
but we've certainly devised some awfully clever computational tools
in recent centuries. (Newton was not only a towering figure in
physics and mathematics, he was a formidable number cruncher. After
inventing an infinite series approximation to the area under a
hyperbola—intimately related to the logarithmic function—he carried
out a calculation of it to 55 decimal places! You can see a page of
this computation in Newton's elegantly precise handwriting on page 39
of James Gleick's Isaac Newton.)
But what seemed to Newton beyond the force of human
intellect—numerically integrating the motion of the planets—no less
doing it over a period of a quarter of a million years—is now
something one can undertake, given a modicum of patience, on a
notebook computer, the present-day embodiment of the
invention of Charles Babbage, Newton's 19th
century successor as Lucasian Professor of Mathematics at Cambridge.
After preliminary
tests and refinement of the analysis tools, on June 26th, 2004 I set
my trusty 2001 vintage 1 GHz Pentium III laptop computer,
lysander.fourmilab.ch
 to work on the numerical integration and transit search. The task was
run as a background process under the
Linux
operating system, with
“nice -9” priority.
to work on the numerical integration and transit search. The task was
run as a background process under the
Linux
operating system, with
“nice -9” priority.
The output produced by each step of the numerical integration consists of 64-bit double precision floating point values for the Julian date of the integration step and the state vector (three-dimensional barycentric position and velocity) of each of the 12 Solar System bodies and pseudo-bodies in the integration. (Although the integration was performed using 80-bit long double quantities, the output of the state at each integration step was configured to use doubles, which are perfectly adequate for the purpose of finding transits). Now that adds up to 73 doubles, or 584 bytes per step, and we're integrating with 100 steps a day, so that's 58,400 bytes of output for each day of the integration, or a tad more than 2 gigabytes per century. Recall that we're integrating for 2500 centuries here—storing the complete results from the numerical integration would require more than 5 terabytes of space, or more than twenty 250 Gb hard drives! (Media cost for storing data offline on tape isn't substantially cheaper per byte than hard drive storage at the present time, and high capacity tape drives [SDLT, Ultrium, AIT-3, etc.] cost a fortune: comparable to twenty hard drives.) I figured that by the time I was likely to do anything more with the numerical integration, I'd have a machine fast enough to re-run the whole shebang in a few weeks, so I opted to scan for transits on the fly and discard the raw results of the integration, much as “cuts” are used in particle physics experiments to reduce the volume of real-time data from the detectors. Filtering for transits limited storage requirements for the entire job to 3.4 Gb, which comfortably fit in the free space on lysander's hard drive, and compressed down to 376 Mb with Gzip for archival storage.
I directed the output of the numerical integrator to a Unix named pipe (or FIFO—first in, first out special file) created with the mkfifo command. This little-known gimmick allows one program to write data which are read by another program without the need to run them as a shell pipeline. Data are transmitted through a memory buffer, and need not be written to disc. The transit search program opens the FIFO for reading and reads its data from there. When the transit finding program gets ahead of data production by the integrator, it goes to sleep until more data arrive; should the integrator get ahead, it goes to sleep until the transit finder consumes some data. The FIFO thus acts as a bounded buffer between the integrator and transit finder. All of this is managed automatically by the operating system, and has the advantage that either program can be run using either the FIFO or disc files without any modification, which is handy for debugging and test cases.
The numerical integrator has the ability to save a checkpoint of its internal state from which the integration can be subsequently resumed. I modified this facility so a checkpoint is saved automatically after each century in the evolution, or when the SIGINT signal is received, avoiding loss of work when it's necessary to shut down the computer. I saved all the checkpoints, and since the integration can be restarted from any of them, this means that if I want to examine the raw integration output for a given time interval (for example, to make a movie of a transit event), I needn't rerun more than a century's integration.
The integration ran more or less continuously on lysander from June 26th to August 20th, 2004—almost two months of computer time. Actually, more than that, since for a month (June 27th to July 30th) I ran the backward integration on another machine, the 400 MHz Pentium II ovni.fourmilab.ch which didn't have anything else to keep it occupied at the time. When lysander completed the forward integration, I moved the backward integration from ovni back to lysander, which would finish it about three times faster. Since I now have checkpoint files which permit restarting the integration at each of the 2500 centuries, should the need arise to re-run it and the task farmed out to run in the background on, say, fifty volunteered 3.4 GHz Pentium 4 machines (which can complete a century of the integration in about 20 minutes), the entire job could be done in less than a day.
The Numerical Integrator
Numerical integration of the solar system is performed using Steve Moshier's DE118i-2 code. This program performs N-body numerical integration of the Sun and planets (including the Earth's Moon), plus the five largest asteroids. The model includes Lunar librations, Earth tides, gravitational harmonics of the Earth and Moon, and corrections for general relativity. Computations are performed using 80-bit floating point quantities. Integration is performed with the Adams-Bashforth-Moulton predictor-corrector algorithm initialised by several Runge-Kutta steps. This computation used an Adams order of 12 and a step size of 1/100 day.
I originally began the project with the August 8th, 2000 release of DE118i-1, then migrated to DE118i-2 which was released on May 13th, 2004, while I was developing the transit finder. A bug which I'd found and fixed in DE118i-1 was corrected in the -2 release; I ported my modifications to save checkpoints to the new release and proceeded with it, after confirming that the output from the two programs was identical for a one century test case.
The initial state vector used for both the forward and backward integration was that included with DE118i, an 18 digit DE118 state vector supplied by JPL with an epoch of Julian day 2440400.5 (June 28.0, 1969—less than a month before Apollo 11 landed on the Moon!). As the integration ran on into deep time, the integrator eventually crashed because the integration step count, which was kept in a 32 bit signed int, wrapped around and went negative after 2,147,483,648 integration steps, or about 58,795 years, I added a kludge to avoid the crash, resumed from the last checkpoint, and encountered no further problems in the rest of the integration. You can download original source code from Steve Moshier's site and my patches from here.
Output from the integrator is in binary floating point format, but you can get an idea of what it involves by examining an integration output file with the dumpres program, included in the Transit Tools download archive. This program simply formats and prints the data from the integrator at each step. The following is the output for a single step. (I have elided six decimal places of precision from each number to make the results fit better on the page.)
JD 2440400.63000 Librations 6.0464e-03 9.9793e-05 3.8239e-01 1.5413e-05 1.2811e+00 -1.1960e-04 Mercury 3.6218e-01 3.1135e-03 -8.7535e-02 2.4958e-02 -8.4025e-02 1.3006e-02 Venus 6.1417e-01 1.0891e-02 -3.4632e-01 1.5652e-02 -1.9445e-01 6.3505e-03 EMB 1.2270e-01 1.6806e-02 -9.2560e-01 1.7822e-03 -4.0143e-01 7.7291e-04 Mars -1.0830e-01 1.4483e-02 -1.3275e+00 2.5873e-04 -6.0592e-01 -2.7409e-04 Jupiter -5.3795e+00 1.0932e-03 -8.3132e-01 -6.5179e-03 -2.2519e-01 -2.8207e-03 Saturn 7.8939e+00 -3.2179e-03 4.5970e+00 4.3355e-03 1.5589e+00 1.9285e-03 Uranus -1.8265e+01 2.2130e-04 -1.1624e+00 -3.7624e-03 -2.5032e-01 -1.6510e-03 Neptune -1.6054e+01 2.6427e-03 -2.3942e+01 -1.4982e-03 -9.4002e+00 -6.7902e-04 Pluto -3.0483e+01 3.2222e-04 -8.7285e-01 -3.1435e-03 8.9114e+00 -1.0779e-03 Moon_Vec -7.2960e-04 6.0756e-04 -2.0153e-03 -1.5082e-04 -1.0977e-03 -7.6482e-05 Sun 4.5047e-03 -3.5335e-07 7.7392e-04 5.1773e-06 2.6879e-04 2.2289e-06
The first line gives the date and time of the integration step as a Julian day number in barycentric dynamical time. Successive lines give, for each object, in three pairs of columns for the X, Y, and Z axes in Solar System barycentric co-ordinates in terms of astronomical units (149,597,870,691 metres) and days (86400 SI seconds), the position and velocity of each body at that step. The “Librations” pseudo-object specifies the three Euler angles in radians of the selenocentric direction of the Earth relative to the Lunar principal moment of inertia axes. “EMB” is the location of the Earth-Moon barycentre (centre of mass), and “Moon_Vec” gives the Solar System barycentric coordinates of the Moon minus those of the Earth; from EMB and Moon_Vec you can compute the positions of the Earth and Moon. Note that a position and velocity is given for the Sun as well; since the origin of the co-ordinate system is the Solar System barycentre, the Sun “orbits” around this point.
The extract.c program, included in the Transit Tools archive,
converts the output of the integrator for a specified range of Julian
days to a CSV format text file easily processed by other programs.
The Transit Finder
Output from the numerical integrator is consumed by the Transit Finder, whose source code transits.c and ancillary files are included in the Transit Tools download archive. At each integration step, for each planet from Venus through Pluto (including the Earth and Moon separately), a vector is projected from the centre of the planet to the centre of the Sun and the instantaneous apparent size of the Sun (neglecting Solar oblateness) is calculated based on the length of this vector. Then, for each planet inward of the current planet, we first test whether the planet is on the same side of the Sun by forming vectors from the Sun to the two planets and taking their dot product; if the sign of the dot product (equal to the cosine of the angle between the two vectors times their lengths) is negative, then the angle between the two Sun/planet vectors is greater than 180° and the planets are on opposite sides of the Sun, excluding the possibility of a transit. Otherwise, a vector is computed from the centre of the outer planet to the centre of the inner planet. Both outer-planet/Sun and outer-planet/inner-planet vectors are normalised to a length of one, so the magnitude of their cross product gives the sine of the angle between them. If this angle is less than the angular radius of the Sun, the inner planet will be in transit across the disc of the Sun as seen from the outer planet.
Note that in performing this calculation we neglect the radius of the inner and outer planets; we only consider a transit in progress if an observer at the centre of the outer planet (or, more practically, on the surface at the point it intersects the planet/Sun vector) sees the centre of the inner planet within the mean apparent solar radius. This excludes extreme graze events which might be visible only from a portion of the outer planet, or miss due to solar oblateness; since such events may also be sufficiently short to start and end between integration steps, attempting to include them would create a false sense of precision. If anybody cares about these marginal events, they could re-run the integration, filter for close misses, and then re-examine them with greater time resolution.
Output from the Transit Finder is simply a list of planets found in transit at each integration step. Here is the output around the 2003 transit of Mercury as seen from the Earth. Again, to make the output fit on the page, I've removed redundant decimal places and the day of the week which occur in the actual output.
Transit of Earth from Neptune 2452488.78 2002-08-02 06:43 0.0089 0.0086 0.0002 Transit of Mercury from Moon 2452766.66 2003-05-07 03:50 0.2645 0.2621 0.0024 Transit of Mercury from Moon 2452766.67 2003-05-07 04:04 0.2645 0.2526 0.0119 Transit of Mercury from Moon 2452766.68 2003-05-07 04:19 0.2645 0.2438 0.0207 Transit of Mercury from Moon 2452766.69 2003-05-07 04:33 0.2645 0.2357 0.0288 Transit of Mercury from Moon 2452766.70 2003-05-07 04:47 0.2645 0.2286 0.0359 Transit of Mercury from Moon 2452766.71 2003-05-07 05:02 0.2645 0.2224 0.0421 Transit of Mercury from Earth 2452766.72 2003-05-07 05:16 0.2642 0.2591 0.0051 Transit of Mercury from Moon 2452766.72 2003-05-07 05:16 0.2645 0.2172 0.0473 Transit of Mercury from Earth 2452766.73 2003-05-07 05:31 0.2642 0.2489 0.0153 Transit of Mercury from Moon 2452766.73 2003-05-07 05:31 0.2645 0.2132 0.0513 Transit of Mercury from Earth 2452766.74 2003-05-07 05:45 0.2642 0.2394 0.0248 Transit of Mercury from Moon 2452766.74 2003-05-07 05:45 0.2645 0.2104 0.0541 Transit of Mercury from Earth 2452766.75 2003-05-07 05:59 0.2642 0.2306 0.0336 Transit of Mercury from Moon 2452766.75 2003-05-07 05:59 0.2645 0.2088 0.0557 Transit of Mercury from Earth 2452766.76 2003-05-07 06:14 0.2642 0.2227 0.0415 Transit of Mercury from Moon 2452766.76 2003-05-07 06:14 0.2645 0.2085 0.0560 Transit of Mercury from Earth 2452766.77 2003-05-07 06:28 0.2642 0.2157 0.0485 Transit of Mercury from Moon 2452766.77 2003-05-07 06:28 0.2645 0.2094 0.0551 Transit of Mercury from Earth 2452766.78 2003-05-07 06:43 0.2642 0.2096 0.0545 Transit of Mercury from Moon 2452766.78 2003-05-07 06:43 0.2645 0.2116 0.0529 Transit of Mercury from Earth 2452766.79 2003-05-07 06:57 0.2642 0.2047 0.0595 Transit of Mercury from Moon 2452766.79 2003-05-07 06:57 0.2645 0.2150 0.0495 Transit of Mercury from Earth 2452766.80 2003-05-07 07:11 0.2642 0.2010 0.0632 Transit of Mercury from Moon 2452766.80 2003-05-07 07:11 0.2645 0.2196 0.0449 Transit of Mercury from Earth 2452766.81 2003-05-07 07:26 0.2642 0.1985 0.0657 Transit of Mercury from Moon 2452766.81 2003-05-07 07:26 0.2645 0.2252 0.0393 Transit of Mercury from Earth 2452766.82 2003-05-07 07:40 0.2642 0.1973 0.0669 Transit of Mercury from Moon 2452766.82 2003-05-07 07:40 0.2645 0.2319 0.0326 Transit of Mercury from Earth 2452766.83 2003-05-07 07:55 0.2642 0.1974 0.0667 Transit of Mercury from Moon 2452766.83 2003-05-07 07:55 0.2645 0.2394 0.0250 Transit of Mercury from Earth 2452766.84 2003-05-07 08:09 0.2642 0.1989 0.0653 Transit of Mercury from Moon 2452766.84 2003-05-07 08:09 0.2645 0.2479 0.0166 Transit of Mercury from Earth 2452766.85 2003-05-07 08:23 0.2642 0.2016 0.0626 Transit of Mercury from Moon 2452766.85 2003-05-07 08:23 0.2645 0.2571 0.0074 Transit of Mercury from Earth 2452766.86 2003-05-07 08:38 0.2642 0.2056 0.0586 Transit of Mercury from Earth 2452766.87 2003-05-07 08:52 0.2642 0.2107 0.0535 Transit of Mercury from Earth 2452766.88 2003-05-07 09:07 0.2642 0.2169 0.0473 Transit of Mercury from Earth 2452766.89 2003-05-07 09:21 0.2642 0.2241 0.0400 Transit of Mercury from Earth 2452766.90 2003-05-07 09:35 0.2642 0.2322 0.0319 Transit of Mercury from Earth 2452766.91 2003-05-07 09:50 0.2642 0.2412 0.0230 Transit of Mercury from Earth 2452766.92 2003-05-07 10:04 0.2642 0.2508 0.0134 Transit of Mercury from Earth 2452766.93 2003-05-07 10:19 0.2642 0.2611 0.0031 Barycentre entering at 2452825.09 2003-07-04 14:09 (G = 1.000, 0.00% of solar radius). Transit of Earth from Neptune 2452855.81 2003-08-04 07:26 0.0089 0.0086 0.0002
The first line is the last step showing the Earth in transit from Neptune in August 2002. (Being the outermost planet which orbits near the ecliptic plane, Neptune not only has more inner planets to observe in transit, its slower orbital velocity provides a longer window of opportunity to catch an inner planet in transit. More transits of each inner planet are visible from Neptune than from any other planet. If you're into transits and don't mind cold weather, it's the place to be.)
Next we begin to see events of the transit of Mercury in May 2003. Note that the transit was first visible from the Moon; Mercury's transit began about an hour and a half later as seen from the Earth. Each record begins with a self-explanatory identification of the transit followed by the Julian day of the integration step, its equivalent in a “proleptic Gregorian calendar and Universal time” which extends arbitrarily backward and forward in time and assumes timekeeping on Earth remains in sync with events in the Solar System, and then the apparent radius, in degrees, of the Sun as seen from the viewing point, the angular distance of the centre of the inner planet from the centre of the Sun, and the “depth” of the transit, which is just the first quantity minus the second. We define the “centre” of the transit as the integration step with the maximum depth; for this transit of Mercury, as seen from Earth, this occurred at 07:40 UTC with a depth of 0.0669 which, within the granularity of the integration, agrees with the actual time of geocentric mid-transit at 07:52:23. As the transit began earlier as seen from the Moon, it ended earlier as well; note that only a transit from the Earth shows up in the last eight integration steps.
Before the next transit item, another transit of Earth from Neptune in August of 2003, there's an item which indicates that the barycentre (centre of mass) of the Solar System, which had earlier been outside the Sun, was now within its mean radius on July 4th, 2003 (set off the fireworks!). The transits program, while watching for transits, also tracks barycentre excursions in order to prepare the list of extrema.
Postprocessing
Output from the Transit Finder is easily postprocessed. The following Perl programs used to analyse the output and create the files published with this page are included in the Transit Tools download archive.
- bary_extrema.pl
- Find extrema (locations closest and farthest from the centre of the Sun) of the Solar System barycentre in output from the bary_minmax_csv.pl program.
- bary_inside_outside.pl
- From the CSV database produced by bary_minmax_csv.pl, compute the number of days and percent of elapsed time the barycentre of the Solar System was inside and outside the Sun.
- bary_local.pl
- Reads the CSV database produced by bary_minmax_csv.pl and generates CSV databases bary_local.csv, the number of minima and maxima between each crossing by the barycentre of the mean solar radius, and bary_local_hist.csv, a histogram of the number of occurrences of each number of minima and maxima.
- bary_minmax_csv.pl
- This program reads the output of Transit Finder and creates bary_minmax.csv, a CSV database of barycentre minima, maxima, and crossings of the mean solar radius. This database is used as input to all the other analyses of the barycentre.
- check_canon_csv.pl
- Sanity check the CSV database created by canonfodder.pl to detect problems in that program or in upstream processing.
- canon_html.pl
- Generate HTML files for the transit databases linked to this page. Input to this program is the CSV database created by canonfodder.pl.
- canonfodder.pl
- Encode output from the Transit Finder as a Comma Separated Value (CSV) canon database. This transit database, transits.csv, is used as input by all analyses of transits.
- extract.c
- Read binary output from the numerical integrator and create a CSV database containing complete data for all integration steps within a specified range of Julian days. This is used to obtain position data for image renderings and movies.
- extract_canon.pl
- Extract records within a specified range of Julian day numbers from the output of the Transit Finder. This allows testing the downstream analysis programs with subsets of the complete data set and isolating test cases for debugging.
- julian.pl
- Julian day to Gregorian and Julian calendar and civil time conversion functions. These calendars are treated as “proleptic”—valid for dates before anybody ever thought of them, and linked to dynamical time (as defined by the motion of the planets, independent of changes in the Earth's rotation rate and orbit).
- mergetrans.pl
- This program merges the output of multiple runs of the numerical integration and Transit Finder, discarding duplicate records which may result from crashes and restarts. The output is a Gzipped master database called all_fine.txt.gz containing only unique records from the raw files.
- patch_clobbered_transit_file.pl
- When you compute for a couple of months, “bit happens”—the disc fills up, the operating system goes bonkers, and Heaven knows what else. If you end up with junk in a file generated by the Transit Finder, this program allows you to replace it with a re-run of the century (or centuries) containing the corrupted data. This is a bespoke program to fix a specific problem—you'll have to modify it for the specifics of your own disasters.
- simultaneous_csv.pl
- Reads the CSV transit database and identifies events in which two or more inner planets are in transit at the same time from an outer planet. Creates the simultaneous.csv database.
- simultaneous_html.pl
- Reads the simultaneous.csv database and creates the HTML document listing simultaneous transits and the simultaneous transit statistics and tables included in this document.
Comparison with Other Catalogues
When performing an extensive calculation like this based on a tiny initial state vector and “billions and billions” of intermediate results, it reduces the “pucker factor” when making the results public to verify them against those independently arrived at by other investigators. Here is a survey of other explorations of transits in the last century and their correspondence with results from this project.
Marth
In the 19th century, Albert Marth calculated numerous transits visible from planets other than the Earth. Citations of his publications and the corresponding entries from this canon for each are given below.
- Marth, Albert. “Note on the Transit of the Earth and Moon across the Sun's Disk as seen from Mars on November 12, 1879, and on some kindred Phenomena”. Monthly Notices of the Royal Astronomical Society, 39 (1879), 513–514.
- Transit of the Earth and Moon from Mars, 1879-11-12, also
transits of the Earth and Moon on 1800-11-08 and in May 1905
and 1984 (no day of the month specified):
Moon 1800-11-08 16:48 G 2378808.09 2378808.20 2378808.31 0.1810 0.1455 Earth 1800-11-09 00:57 G 2378808.38 2378808.54 2378808.69 0.1810 0.1050 Moon 1879-11-12 17:31 G 2407666.08 2407666.23 2407666.39 0.1804 0.1162 Earth 1879-11-12 19:55 G 2407666.17 2407666.33 2407666.49 0.1804 0.0963 * Earth 1905-05-08 20:09 G 2416974.16 2416974.34 2416974.51 0.1717 0.0774 Moon 1905-05-09 01:55 G 2416974.41 2416974.58 2416974.75 0.1718 0.0901 * Earth 1984-05-11 08:38 G 2445831.69 2445831.86 2445832.03 0.1722 0.0851 Moon 1984-05-11 14:09 G 2445831.95 2445832.09 2445832.22 0.1723 0.1141 *
- Ten transits of Mercury from Mars, specified by year, month, and day as follows:
Mercury 1836-07-28 10:19 G 2391853.82 2391853.93 2391854.04 0.1821 0.0702 Mercury 1837-08-23 17:02 G 2392245.06 2392245.21 2392245.36 0.1721 0.0712 Mercury 1838-07-03 20:38 G 2392559.34 2392559.36 2392559.37 0.1793 0.1764 Mercury 1847-01-13 16:04 G 2395675.00 2395675.17 2395675.33 0.1714 0.0206 Mercury 1847-11-24 06:14 G 2395989.67 2395989.76 2395989.84 0.1800 0.1186 Mercury 1856-06-04 15:35 G 2399105.02 2399105.15 2399105.28 0.1707 0.1081 Mercury 1857-04-15 15:35 G 2399420.05 2399420.15 2399420.26 0.1807 0.0600 Mercury 1866-09-06 01:11 G 2402850.43 2402850.55 2402850.66 0.1814 0.0060 Mercury 1876-01-27 10:19 G 2406280.82 2406280.93 2406281.04 0.1822 0.0643 Mercury 1877-02-21 17:45 G 2406672.10 2406672.24 2406672.39 0.1721 0.0814Marth, however, missed the following transit of Mercury from Mars:
Mercury 1845-12-18 19:11 G 2395284.22 2395284.30 2395284.38 0.1829 0.1353
- Four transits of Venus from Mars:
Venus 1830-05-15 18:28 G 2389588.14 2389588.27 2389588.40 0.1858 0.1239 Venus 1834-12-27 09:07 G 2391274.72 2391274.88 2391275.04 0.1669 0.0605 Venus 1862-05-15 14:38 G 2401275.95 2401276.11 2401276.28 0.1870 0.0693 Venus 1866-12-26 05:02 G 2402961.55 2402961.71 2402961.88 0.1660 0.0502
- Transits of Mars from Jupiter, Saturn, Uranus, and Neptune:
Jupiter 1785-08-13 06:14 G 2373242.53 2373242.76 2373243.00 0.0538 0.0204 Saturn 1831-07-25 15:07 G 2390024.02 2390024.13 2390024.26 0.0287 0.0265 Saturn 1847-07-26 18:43 G 2395869.03 2395869.28 2395869.54 0.0274 0.0086 Uranus 1851-07-25 21:50 G 2397329.13 2397329.41 2397329.71 0.0134 0.0021 Uranus 1853-06-25 05:16 G 2398029.54 2398029.72 2398029.90 0.0135 0.0106 Neptune 1860-10-25 20:24 G 2400709.14 2400709.35 2400709.62 0.0089 0.0050 Neptune 1862-09-19 15:07 G 2401402.88 2401403.13 2401403.41 0.0089 0.0037 Jupiter 1886-04-13 19:11 G 2410010.02 2410010.30 2410010.60 0.0489 0.0112
- Transit of the Earth and Moon from Mars, 1879-11-12, also
transits of the Earth and Moon on 1800-11-08 and in May 1905
and 1984 (no day of the month specified):
- Marth, Albert. “Note on the Transit of the Planet Mars and its Satellites across the Sun's disc, which will occur for the Planet Jupiter and its Satellites on April 13, 1886”. Monthly Notices of the Royal Astronomical Society, 46 (1886), 161–164.
- Transit of Mars from Jupiter:
Mars 1886-04-13 19:11 G 2410010.02 2410010.30 2410010.60 0.0489 0.0112
- Transits of Mercury from Jupiter:
Mercury 1833-12-02 06:57 G 2390884.67 2390884.79 2390884.91 0.0537 0.0210 Mercury 1834-03-01 14:52 G 2390974.03 2390974.12 2390974.20 0.0535 0.0396 Mercury 1840-01-16 08:24 G 2393120.68 2393120.85 2393121.02 0.0491 0.0134 Mercury 1845-09-20 10:19 G 2395194.83 2395194.93 2395195.02 0.0537 0.0366 Mercury 1845-12-18 18:28 G 2395284.16 2395284.27 2395284.38 0.0535 0.0245 Mercury 1851-11-04 06:57 G 2397430.65 2397430.79 2397430.94 0.0491 0.0296 Mercury 1852-02-02 11:45 G 2397520.88 2397520.99 2397521.11 0.0492 0.0374 Mercury 1857-07-09 13:26 G 2399505.04 2399505.06 2399505.09 0.0537 0.0526 Mercury 1857-10-06 22:04 G 2399594.29 2399594.42 2399594.55 0.0536 0.0092 Mercury 1863-08-23 06:00 G 2401740.69 2401740.75 2401740.82 0.0490 0.0453 Mercury 1863-11-21 10:04 G 2401830.76 2401830.92 2401831.09 0.0491 0.0208 Mercury 1869-07-26 00:57 G 2403904.41 2403904.54 2403904.67 0.0537 0.0072 Mercury 1869-10-23 08:38 G 2403993.85 2403993.86 2403993.88 0.0535 0.0528 Mercury 1875-09-09 08:24 G 2406140.68 2406140.85 2406141.03 0.0491 0.0041 Mercury 1881-05-14 04:33 G 2408214.58 2408214.69 2408214.81 0.0537 0.0223 Mercury 1881-08-11 12:43 G 2408303.94 2408304.03 2408304.12 0.0535 0.0385 Mercury 1887-06-28 06:14 G 2410450.59 2410450.76 2410450.93 0.0491 0.0135There was a typographical error in the entry for the 1887 transit; the month was given as “Aug.”, when clearly June was intended. - Transits of Venus from Jupiter:
Venus 1834-12-08 00:28 G 2391255.37 2391255.52 2391255.66 0.0528 0.0370 Venus 1840-10-03 09:35 G 2393381.77 2393381.90 2393382.04 0.0496 0.0375 Venus 1846-08-12 15:07 G 2395520.93 2395521.13 2395521.33 0.0529 0.0018 Venus 1853-01-30 18:28 G 2397884.19 2397884.27 2397884.36 0.0500 0.0448 Venus 1858-04-17 05:16 G 2399786.59 2399786.72 2399786.85 0.0531 0.0410 Venus 1864-10-05 18:57 G 2402150.09 2402150.29 2402150.48 0.0498 0.0127 Venus 1876-06-10 19:55 G 2406416.15 2406416.33 2406416.52 0.0496 0.0191 Venus 1882-04-20 05:45 G 2408555.55 2408555.74 2408555.92 0.0529 0.0203 - Transits of Earth and Moon from Jupiter:
Moon 1752-12-31 18:43 G 2361330.05 2361330.28 2361330.50 0.0514 0.0144 Earth 1752-12-31 21:21 G 2361330.17 2361330.39 2361330.61 0.0514 0.0153 * Earth 1765-01-05 11:16 G 2365717.83 2365717.97 2365718.11 0.0511 0.0398 Moon 1765-01-05 12:28 G 2365717.87 2365718.02 2365718.18 0.0511 0.0368 * Earth 1806-06-25 17:02 G 2380863.02 2380863.21 2380863.42 0.0510 0.0282 Moon 1806-06-25 20:38 G 2380863.18 2380863.36 2380863.55 0.0510 0.0307 * Earth 1811-12-23 20:24 G 2382870.21 2382870.35 2382870.50 0.0518 0.0396 Moon 1811-12-24 00:00 G 2382870.35 2382870.50 2382870.66 0.0518 0.0377 * Moon 1818-06-30 11:16 G 2385250.73 2385250.97 2385251.22 0.0512 0.0013 Earth 1818-06-30 13:40 G 2385250.83 2385251.07 2385251.31 0.0512 0.0027 * Moon 1823-12-28 10:04 G 2387257.69 2387257.92 2387258.15 0.0516 0.0113 Earth 1823-12-28 12:57 G 2387257.82 2387258.04 2387258.26 0.0516 0.0140 * Earth 1830-07-05 11:45 G 2389638.78 2389638.99 2389639.20 0.0514 0.0232 Moon 1830-07-05 12:14 G 2389638.82 2389639.01 2389639.21 0.0514 0.0262 * Earth 1836-01-02 04:04 G 2391645.44 2391645.67 2391645.89 0.0514 0.0113 Moon 1836-01-02 05:16 G 2391645.51 2391645.72 2391645.94 0.0514 0.0102 * Earth 1842-07-10 12:28 G 2394026.96 2394027.02 2394027.07 0.0516 0.0500 Moon 1842-07-10 14:09 G 2394027.02 2394027.09 2394027.18 0.0516 0.0484 * Moon 1848-01-06 15:21 G 2396032.97 2396033.14 2396033.33 0.0512 0.0324 Earth 1848-01-06 15:21 G 2396032.98 2396033.14 2396033.31 0.0512 0.0354 * Moon 1889-06-24 16:33 G 2411178.01 2411178.19 2411178.37 0.0510 0.0352 Earth 1889-06-24 19:11 G 2411178.12 2411178.30 2411178.48 0.0510 0.0327 * Moon 1931-01-06 15:50 G 2426347.98 2426348.16 2426348.35 0.0513 0.0279 Earth 1931-01-06 17:45 G 2426348.05 2426348.24 2426348.42 0.0513 0.0304 * - Transits of Jupiter from outer planets:
Uranus 1789-05-10 21:50 G 2374609.10 2374609.41 2374609.77 0.0144 0.0111 Uranus 1914-05-03 04:04 G 2420255.17 2420255.67 2420256.19 0.0134 0.0010
Marth computes transits of Jupiter from Uranus for “mid-summer 1706” and 1997 as well. I did not find these transits; either they are grazes, or perhaps the orbit of Uranus was not known sufficiently accurately in Marth's day to exclude them. - Transits of Jupiter from Neptune:
Neptune 2188-08-08 06:43 G 2520430.34 2520430.78 2520431.28 0.0089 0.0039
Marth makes no explicit predictions, since the orbit of Neptune was not sufficiently well known and even given better tables would require “stricter computations than I have made”. He suggests the possibility of transits at the conjunctions of 1613, 1779, 2022, and 2188. In fact, a transit occurs only at the 2188 conjunction listed above. - Transits of Jupiter from Saturn. Marth calculates, based on the tables
of Le Verrier, that no transit of Jupiter from Saturn occurs in in the
last or next 2000 years from the 1886 date of his paper. This is
almost correct, but not quite. In fact, a transit of Jupiter
from Saturn occurred in the year 86 BCE, which is 1971 years (recall there's
no year 0 in our Julian calendar) before his paper. Here are the last and
next transits of Jupiter from Saturn, valid both for his time and ours.
Jupiter -86-09-16 18:14 J 1690270.03 1690270.26 1690270.52 0.0289 0.0247 Jupiter 7541-03-18 00:43 G 4475429.14 4475429.53 4475429.96 0.0286 0.0118
- Transit of Mars from Jupiter:
- Marth, Albert. “Note on the Transit of Mercury over the Sun's Disc, which takes place for Venus on 1894 March 21, and on the Transits of Venus and Mercury, which occur for Saturn's System on the same day”. Monthly Notices of the Royal Astronomical Society, 54 (1894), 172–174.
- Transit of Mercury from Venus:
Mercury 1894-03-22 00:28 G 2412909.45 2412909.52 2412909.59 0.3693 0.3183
- Transit of Mercury and Venus from Saturn:
Venus 1894-03-21 08:38 G 2412908.74 2412908.86 2412908.98 0.0275 0.0223 Mercury 1894-03-21 17:02 G 2412909.17 2412909.21 2412909.26 0.0275 0.0264
- Transits of Mercury from Venus:
Mercury 1843-03-01 04:19 G 2394260.54 2394260.68 2394260.82 0.3692 0.0971 Mercury 1847-02-28 07:55 G 2395720.74 2395720.83 2395720.92 0.3678 0.1927 Mercury 1848-09-14 09:21 G 2396284.78 2396284.89 2396285.00 0.3691 0.2429 Mercury 1852-09-13 00:28 G 2397744.42 2397744.52 2397744.63 0.3679 0.0522 Mercury 1858-03-29 17:02 G 2399768.10 2399768.21 2399768.31 0.3679 0.0867 Mercury 1863-10-13 09:21 G 2401791.80 2401791.89 2401791.97 0.3680 0.2212 Mercury 1894-03-22 00:28 G 2412909.45 2412909.52 2412909.59 0.3693 0.3183
Marth missed the following 1869 transit, probably because it was so close to a graze.Mercury 1869-04-28 01:26 G 2403815.54 2403815.56 2403815.59 0.3681 0.3535
- Transits of Mercury from Saturn:
Mercury 1835-06-15 16:48 G 2391445.08 2391445.20 2391445.33 0.0275 0.0186 Mercury 1835-09-12 12:43 G 2391533.85 2391534.03 2391534.21 0.0274 0.0041 Mercury 1835-12-10 08:38 G 2391622.70 2391622.86 2391623.03 0.0273 0.0105 Mercury 1836-03-08 05:02 G 2391711.65 2391711.71 2391711.78 0.0273 0.0252 Mercury 1851-01-05 15:35 G 2397128.07 2397128.15 2397128.24 0.0286 0.0216 Mercury 1851-04-04 04:19 G 2397216.55 2397216.68 2397216.81 0.0286 0.0089 Mercury 1851-07-01 16:48 G 2397305.07 2397305.20 2397305.34 0.0287 0.0038 Mercury 1851-09-28 05:16 G 2397393.61 2397393.72 2397393.83 0.0288 0.0164 Mercury 1864-11-01 17:31 G 2402177.13 2402177.23 2402177.33 0.0275 0.0222 Mercury 1865-01-29 13:11 G 2402265.88 2402266.05 2402266.22 0.0274 0.0077 Mercury 1865-04-28 09:21 G 2402354.71 2402354.89 2402355.06 0.0273 0.0069 Mercury 1865-07-26 05:31 G 2402443.62 2402443.73 2402443.84 0.0273 0.0216 Mercury 1880-05-24 18:57 G 2407860.22 2407860.29 2407860.37 0.0285 0.0240 Mercury 1880-08-21 07:40 G 2407948.70 2407948.82 2407948.95 0.0286 0.0113 Mercury 1880-11-17 20:24 G 2408037.21 2408037.35 2408037.48 0.0286 0.0015 Mercury 1881-02-14 08:38 G 2408125.75 2408125.86 2408125.98 0.0287 0.0139 Mercury 1881-05-13 20:52 G 2408214.33 2408214.37 2408214.43 0.0288 0.0264 Mercury 1894-03-21 17:02 G 2412909.17 2412909.21 2412909.26 0.0275 0.0264 Mercury 1894-06-18 12:43 G 2412997.87 2412998.03 2412998.19 0.0274 0.0120 Mercury 1894-09-15 08:38 G 2413086.68 2413086.86 2413087.04 0.0274 0.0026 Mercury 1894-12-13 04:33 G 2413175.56 2413175.69 2413175.84 0.0273 0.0172
Marth shows a transit of Mercury from Saturn on 1851-12-23.3 which does not appear in this canon. I have not investigated whether it is a graze or is not a transit at all. - Transits of Venus from Saturn:
Venus 1835-10-14 05:16 G 2391565.52 2391565.72 2391565.93 0.0274 0.0069 Venus 1836-05-30 11:02 G 2391794.78 2391794.96 2391795.15 0.0272 0.0140 Venus 1851-06-23 06:43 G 2397296.58 2397296.78 2397296.99 0.0287 0.0059 Venus 1852-02-08 01:40 G 2397526.42 2397526.57 2397526.74 0.0289 0.0190 Venus 1864-09-08 04:19 G 2402122.60 2402122.68 2402122.77 0.0275 0.0251 Venus 1865-04-25 11:31 G 2402351.77 2402351.98 2402352.19 0.0273 0.0038 Venus 1865-12-10 17:16 G 2402581.06 2402581.22 2402581.39 0.0272 0.0170 Venus 1880-05-17 23:31 G 2407853.41 2407853.48 2407853.58 0.0285 0.0260 Venus 1881-01-02 17:31 G 2408083.02 2408083.23 2408083.44 0.0287 0.0019 Venus 1881-08-20 12:28 G 2408312.90 2408313.02 2408313.15 0.0289 0.0229 Venus 1894-03-21 08:38 G 2412908.74 2412908.86 2412908.98 0.0275 0.0223 Venus 1894-11-05 15:21 G 2413137.93 2413138.14 2413138.35 0.0273 0.0011 Venus 1895-06-22 20:38 G 2413367.23 2413367.36 2413367.52 0.0272 0.0197
- Transit of Mercury from Venus:
Meeus
Jean Meeus published a list of transits of the Earth as seen from Mars in the Journal of the British Astronomical Association in 1983. The transit of Earth of November 10th, 2084 inspired Arthur C. Clarke's 1971 story Transit of Earth.
- Meeus, Jean and Edwin Goffin. “Transits of Earth as Seen from Mars”, Journal of the British Astronomical Association, 93 (1983), 120–123.
- Transits of the Earth as seen from Mars, −4 to 3015:
-5-04-25 19:40 J 1719712.14 1719712.32 1719712.49 0.1775 0.0854 75-04-29 16:04 J 1748570.02 1748570.17 1748570.31 0.1781 0.1178 175-10-28 22:04 J 1785277.25 1785277.42 1785277.60 0.1759 0.0592 254-10-31 10:47 J 1814134.81 1814134.95 1814135.10 0.1753 0.1090 280-04-26 00:28 J 1823443.34 1823443.52 1823443.70 0.1767 0.0694 359-04-29 19:40 J 1852301.19 1852301.32 1852301.46 0.1773 0.1275 459-10-29 12:28 J 1889008.84 1889009.02 1889009.21 0.1766 0.0296 538-11-01 01:55 J 1917866.47 1917866.58 1917866.69 0.1760 0.1424 564-04-26 05:45 J 1927174.55 1927174.74 1927174.93 0.1759 0.0523 643-04-30 00:14 J 1956032.39 1956032.51 1956032.63 0.1765 0.1391 743-10-30 00:57 J 1992740.35 1992740.54 1992740.73 0.1773 0.0038 822-11-01 15:35 J 2021598.12 2021598.15 2021598.18 0.1768 0.1735 848-04-26 12:14 J 2030905.82 2030906.01 2030906.21 0.1751 0.0329 927-04-30 05:31 J 2059763.64 2059763.73 2059763.82 0.1757 0.1533 948-10-26 21:35 J 2067614.32 2067614.40 2067614.49 0.1787 0.1599 1027-10-30 12:43 J 2096471.84 2096472.03 2096472.22 0.1781 0.0229 1132-04-26 20:24 J 2134637.15 2134637.35 2134637.54 0.1744 0.0106 1211-04-30 12:57 J 2163495.02 2163495.04 2163495.07 0.1749 0.1726 1232-10-27 07:11 J 2171345.68 2171345.80 2171345.92 0.1795 0.1407 1311-10-31 00:14 J 2200203.32 2200203.51 2200203.69 0.1789 0.0488 1337-04-24 16:19 J 2209511.09 2209511.18 2209511.27 0.1731 0.1533 1416-04-27 06:43 J 2238368.59 2238368.78 2238368.98 0.1736 0.0186 1516-10-27 16:33 J 2275077.05 2275077.19 2275077.33 0.1802 0.1220 1595-11-10 10:33 G 2303934.77 2303934.94 2303935.12 0.1796 0.0737 1621-05-05 05:16 G 2313242.58 2313242.72 2313242.86 0.1724 0.1167 1700-05-08 19:26 G 2342100.12 2342100.31 2342100.49 0.1729 0.0511 1800-11-09 00:57 G 2378808.38 2378808.54 2378808.69 0.1810 0.1050 1879-11-12 19:55 G 2407666.17 2407666.33 2407666.49 0.1804 0.0963 1905-05-08 20:09 G 2416974.16 2416974.34 2416974.51 0.1717 0.0774 1984-05-11 08:38 G 2445831.69 2445831.86 2445832.03 0.1722 0.0851 2084-11-10 06:00 G 2482539.59 2482539.75 2482539.92 0.1818 0.0951 2163-11-15 03:21 G 2511397.49 2511397.64 2511397.78 0.1812 0.1140 2189-05-10 11:16 G 2520705.78 2520705.97 2520706.16 0.1711 0.0380 2268-05-13 22:48 G 2549563.32 2549563.45 2549563.59 0.1716 0.1204 2368-11-13 09:21 G 2586270.72 2586270.89 2586271.06 0.1826 0.0902 2394-05-10 14:38 G 2595580.04 2595580.11 2595580.19 0.1699 0.1547 2447-11-17 07:26 G 2615128.67 2615128.81 2615128.95 0.1820 0.1248 2473-05-13 01:55 G 2624437.39 2624437.58 2624437.77 0.1704 0.0003 2552-05-16 13:26 G 2653294.99 2653295.06 2653295.14 0.1709 0.1558 2652-11-15 11:02 G 2690001.79 2690001.96 2690002.13 0.1835 0.0890 2678-05-13 08:09 G 2699311.69 2699311.84 2699311.98 0.1693 0.1110 2731-11-20 09:50 G 2718859.78 2718859.91 2718860.04 0.1828 0.1315 2757-05-16 18:00 G 2728169.06 2728169.25 2728169.44 0.1698 0.0396 2936-11-17 10:48 G 2793732.78 2793732.95 2793733.12 0.1843 0.0928 2962-05-16 02:24 G 2803043.43 2803043.60 2803043.78 0.1687 0.0656 3015-11-22 11:16 G 2822590.85 2822590.97 2822591.10 0.1837 0.1359Note that the transit Meeus lists as “−4-04-25” is, in our historian-style interpretation of the Julian calendar, “−5-04-25”.
- Transits of the Earth as seen from Mars, −4 to 3015:
SOLEX
Prior to the publication of this document, the largest catalogue of transits of which I am aware as produced by Prof. Aldo Vitagliano, developer of the SOLEX numerical integration software for Windows. In 2003 he published lists of transits of Mercury for the years ±50,000 and Venus for years ±100,000. I wrote a program to compare his catalogues (which I'll call the Canon SOLEX) with the Earth/Mercury and Earth/Venus events in this canon with the following results. Every event in this canon appears in Canon SOLEX with a mean absolute value time difference for the moment of maximum transit of 573 seconds for the transits of Venus and 350 seconds for the transits of Mercury. This discrepancy is well within the expected range given the 1/100 day, or 864 second integration step size used in preparing this canon. A total of 148 transits of Venus and 187 transits of Mercury which appear in Canon SOLEX do not figure in the present canon. I examined each of the discrepancies which fall into the period covered by the lists of transits in Jean Meeus's Astronomical Tables of the Sun, Moon and Planets, and each was either a grazing event or a near graze whose transit time was less than the integration step size used in this study, explaining its absence from this canon.
Transit Trivia
One of the great things about amassing a huge pile of data is that you can “mine” it to answer arcane questions which pop into your head. The following, presented in question and answer form, are various items of trivia I've found examining the canon. I'll add to this list as I make additional discoveries or readers share their own with me.
- What is the shortest interval between two transits of Mercury seen from the Earth?
- In March of the years −124413 and −124412, two consecutive
transits of Mercury occur 348.95 days—less than a year—apart.
Mercury makes three orbits of the Sun between these transits,
both of which are relatively near the limb of the Sun.
-124413-03-17 21:08 J -43720348.62 -43720348.62 -43720348.61 0.2779 0.2767 -124412-03-01 21:37 J -43719999.67 -43719999.60 -43719999.54 0.2779 0.2154
- What is the longest interval between transits of Venus seen from the Earth?
- Starting on −119059-01-10 a series of 18 transits of Venus
occur in alternating periods of 73.53 and 169.48 years.
The latter is the the longest period between transits of
Venus in the canon.
-119059-01-10 13:13 J -41764867.12 -41764866.95 -41764866.79 0.2635 0.0162 -118890-07-02 14:10 J -41702967.06 -41702966.91 -41702966.75 0.2710 0.0554 -118816-01-10 12:01 J -41676111.16 -41676111.00 -41676110.83 0.2632 0.0186 -118647-07-02 17:46 J -41614210.92 -41614210.76 -41614210.61 0.2713 0.0389 -118573-01-11 11:17 J -41587355.20 -41587355.03 -41587354.87 0.2628 0.0226 -118404-07-02 20:39 J -41525454.79 -41525454.64 -41525454.49 0.2716 0.0279 -118330-01-11 10:34 J -41498599.23 -41498599.06 -41498598.90 0.2625 0.0294 -118161-07-02 23:46 J -41436698.66 -41436698.51 -41436698.36 0.2720 0.0148 -118087-01-11 09:51 J -41409843.26 -41409843.09 -41409842.93 0.2621 0.0348 -117918-07-04 02:24 J -41347942.55 -41347942.40 -41347942.25 0.2723 0.0073 -117844-01-11 09:36 J -41321087.27 -41321087.10 -41321086.94 0.2618 0.0461 -117675-07-04 05:17 J -41259186.43 -41259186.28 -41259186.13 0.2726 0.0028 -117601-01-12 08:53 J -41232331.29 -41232331.13 -41232330.97 0.2615 0.0538 -117432-07-04 07:41 J -41170430.33 -41170430.18 -41170430.03 0.2729 0.0073 -117358-01-12 08:53 J -41143575.29 -41143575.13 -41143574.97 0.2612 0.0671 -117189-07-04 10:20 J -41081674.22 -41081674.07 -41081673.92 0.2733 0.0138 -117115-01-12 08:53 J -41054819.29 -41054819.13 -41054818.98 0.2608 0.0797 -116946-07-05 12:29 J -40992918.13 -40992917.98 -40992917.83 0.2736 0.0154
- What is the longest interval in which no transit is visible from any planet in the Solar System?
- Between the transit of Mercury visible from Jupiter on
116523-06-29 and that visible from Saturn on 116529-08-09,
a total of 2232.12 days—more than six years—elapse.
Jupiter 116523-06-29 19:39 G 44280391.19 44280391.32 44280391.44 0.0532 0.0158 Saturn 116529-08-09 03:20 G 44282623.56 44282623.64 44282623.72 0.0275 0.0242
- What is the maximum number of transits which occur in the Solar System in a single week?
- In the week beginning on −90353-02-01 13:54, a total
of eight transits occur. Three transits of Mercury
from the Moon, Earth, and Saturn:
Moon -90353-02-01 16:03 J -31279978.92 -31279978.83 -31279978.73 0.2743 0.1557 Earth -90353-02-01 16:32 J -31279978.91 -31279978.81 -31279978.72 0.2749 0.1523 * Saturn -90353-02-03 01:39 J -31279977.55 -31279977.43 -31279977.31 0.0275 0.0157
then three transits of Venus from the same three planets:Earth -90353-02-07 08:23 J -31279973.31 -31279973.15 -31279973.00 0.2743 0.0372 Moon -90353-02-07 13:11 J -31279973.11 -31279972.95 -31279972.80 0.2740 0.0619 * Saturn -90353-02-07 22:47 J -31279972.75 -31279972.55 -31279972.34 0.0275 0.0073
followed by transits of the Earth and Moon from Saturn:Moon -90353-02-08 04:47 J -31279972.54 -31279972.30 -31279972.07 0.0275 0.0027 * Earth -90353-02-08 07:54 J -31279972.41 -31279972.17 -31279971.93 0.0275 0.0012 *
Download Centre
Warning: The data available here were produced by a computation involving more than 9 billion numerical integration steps and trillions of floating point operations, carried out over a period of almost two months. In numerical integration, the output of each step is input to the next; any error propagates into all subsequent results. There is no way to exclude the possibility of error, either hardware or software, in a computation like this without performing it a second time, ideally on different hardware with a different integration code. I have not done this, and I do not in any way certify these results as error-free. Further, even if the numerical integration produces perfect results, and the accuracy of the initial state vector and integration faithfully model the Solar System over such an extended period of time, there are many ways to mess up in the downstream analysis of the integration, many of which I have personally experienced over the last few months. I deliberately limited the scope of the transits.c program which performed real-time analysis of the integration results because any error there would require re-running the entire job. If the integration results and transit and barycentre analysis by transits.c are correct, any errors in subsequent results can be remedied by correcting and re-running the downstream Perl programs, which takes a couple of hours at most. I invite independent confirmation or refutation of these results, but I cannot provide assistance to such a project.
So, before you book your trip to Saturn to see the triple transit of Venus, Earth, and Moon in December 23364, you might want to hold off a tad and see if these results stand up to independent scrutiny.
The following links allow you to download the canon databases in various forms, along with the software tools used to compute them and produce this document. The software tools developed for this project are in the public domain and may be used in any manner without restrictions, but they are utterly unsupported; you are entirely on your own. Please see the ssystem.doc file which accompanies the DE118i-2 numerical integrator code for information regarding its use.
- Complete Canon Transit Database
The following links provide identical data in different forms of compression and text file formats. Download only one!- transits.tar.bz2: bzip2 compressed Unix EOL, 12.3 Mb
- transits.tar.gz: gzip compressed Unix EOL, 14.0 Mb
- transits.zip: zip compressed Windows/MS-DOS EOL, 13.7 Mb
- Simultaneous Transits
- Catalogue of Simultaneous Transits
- simultaneous.zip: zip archive containing simultaneous transit database, CSV file, 8 Kb
- a26982532.gif: Movie of the simultaneous transit of Mercury and Venus visible from the Earth in the year 69163, 150 Kb animated GIF. Right click and use “Save Link” (or whatever) to download and save to your computer.
- Barycentre Data
- barycentre.zip: zip Archive containing CSV databases of all barycentre minima, maxima, and crossings of the mean solar radius; extreme excursions; the number of minima and maxima between each crossing of the mean solar radius; and a histogram of the frequency of the latter. 1.7 Mb.
- Numerical Integration Code
- DE118i-2 numerical integrator from Steve Moshier's site: de118i-2.zip, 258 Kb, zip archive.
- My patches to DE118i-2 to implement checkpoints and permit integrating beyond 231 steps: de118-2_modifications.tar.gz, 5 Kb gzip compressed Unix TAR archive.
- Transit Tools
- Transit Finder program and Perl utilities to postprocess its output: transit_canon_tools.tar.gz, 26 Kb gzip compressed Unix TAR archive.
- Image and Movie Generation
Note: The movie and image generation tools are the crudest of brutal, one-off hacks. They assume all kinds of things about your system configuration, working directory structure, and the presence of the utilities they use. The programs are configured by modifying the source code, and doing so not only requires familiarity with Perl, but with the arcane command line options of the utilities and the scene definition language of the ray tracer. There is essentially zero chance of these programs working “out of the box”—you're going to have to fiddle them at the very least. Still, if you just can't avert your eyes, here they are.- movie_tools.tar.gz,
177 Kb gzip compressed Unix
TAR archive.
The image and movie generation tools require the following free software packages:
- movie_tools.tar.gz,
177 Kb gzip compressed Unix
TAR archive.
Glossary
Terms in this glossary are defined as applicable to and used in this document, not in full generality.
- analytical planetary theory
- Model of planetary motion in which positions of planets may be calculated directly for a given date, as opposed to numerical integration, in which all intermediate positions between a known starting point and the desired date must be calculated. Analytical planetary theories are accurate only over a limited time interval around a specific date.
- astronomical unit (AU)
- The mean distance between the Earth and the Sun. Defined as 149,597,870,691 metres.
- barycentre
- The centre of mass of a collection of bodies.
- barycentric coordinate time (TCB)
- Time as would be measured by an atomic clock measuring SI seconds located at the barycentre of the Solar System, but free of gravitational influences due to general relativity.
- Comma Separated Value (CSV)
- Computer file format consisting of lines of text in which data fields are separated by the comma (“,”) character. Conventions exist for embedding commas within fields and other special cases, but are not required by files used in this project.
- Common Era (CE)
- Politically correct replacement for A.D. Likewise, BCE is the replacement for B.C. Note that there is an ambiguity regarding years before 1 CE; the year prior to 1 CE in the Julian calendar has traditionally been denoted 1 BCE, skipping year zero. To simplify arithmetic, astronomers often denote 1 CE as year +1, and 1 BCE as year 0. Hence in this system year −123 would be year 124 BCE. We use the historical convention for dates in the Julian calendar in this document: the year 1 (1 CE) is immediately preceded by year −1 (1 BCE); there is no year 0.
- conjunction, inferior
- Closest approach of one planet to another; when an inner planet is between the Sun and an outer planet. A transit can occur only at inferior conjunction.
- conjunction, superior
- Greatest distance of one planet from another; occurs when the Sun is between the two planets.
- Earth-Moon Barycentre (EMB)
- Centre of mass of the Earth-Moon system. The Earth is about 81 times as massive as the Moon, and the barycentre of the two bodies is always within the Earth.
- ecliptic
- Plane defined by the Earth's orbit around the Sun. Transits of Mercury and Venus occur only when inferior conjunction closely coincides with their passage through the ecliptic.
- general relativity
- Einstein's 1915 geometric theory of gravitation. Clocks run slower when in a gravitational field, and orbits around massive objects depart from Keplerian elliptical paths. General relativity is particularly important when calculating the orbit of the planet Mercury.
- Gregorian calendar
- Calendar proclaimed in 1582 by Pope Gregory XIII, now used as the civil calendar in most of the world. Note that the Gregorian calendar was adopted at different dates in different countries. We express dates starting with October 15th, 1582 (Julian day 2299160.5) in the Gregorian calendar and prior dates in the Julian calendar.
- integration, numerical
- Approximate evaluation of an integral by stepwise computation. In n-body gravitation problems, the forces, accelerations, velocities, and positions of bodies are updated in discrete integration steps.
- integration step
- Simulation time interval between updates of state in a numerical integration. The Solar System integration in this project used an integration step of 1/100 of a day, or 14.4 minutes.
- Julian calendar
- Calendar introduced by Julius Cæsar and used from Roman times until adoption of the Gregorian calendar in 1582 or later. In the Julian calendar every fourth year is a leap year.
- Julian day (or date)
- Time in days and fraction of a day since January 1, 4713 BCE, at noon Greenwich time. Note that the Julian day number has nothing whatsoever to do with the Julian calendar.
- leap second
- Second added to the UTC terrestrial time standard to keep it in synchronisation with the Earth's rotation.
- proleptic
- Extension of a calendar to dates before it was adopted or used. Negative Julian day numbers and expressing dates in the Julian calendar prior to its adoption in 46 BCE are examples of proleptic calendars.
- second, SI
- Duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cæsium 133 atom.
- special relativity
- Einstein's 1905 theory of the kinematics and electrodynamics of moving bodies. Clocks moving relative to an observer are seen to run slower than clocks stationary with respect to the observer, and there is no way, in general, to define simultaneity of events for spatially separated observers.
- state vector
- In numerical integration of the Solar System, the positions and velocities of all bodies at a specific integration step.
- transit, planetary
- Passage of an in inner planet in front of the disc of the Sun as seen from an outer planet. From the Earth, transits of Mercury and Venus may be observed.
- UTC
- Coordinated Universal Time. Terrestrial time standard based on the Greenwich meridian, adjusted to remain in synchronism with the Earth's rotation by the addition of leap seconds as necessary.
November 27, 2004