Mathematics

Aczel, Amir D. The Mystery of the Aleph. New York: Four Walls Eight Windows, 2000. ISBN 1-56858-105-X.

July 2001 

Barrow, John D. The Book of Nothing. New York: Pantheon Books, 2000. ISBN 0-375-42099-1.

May 2001 

Barrow, John D. The Infinite Book. New York: Vintage Books, 2005. ISBN 1-4000-3224-5.

Don't panic—despite the title, this book is only 330 pages! Having written an entire book about nothing (The Book of Nothing, May 2001), I suppose it's only natural the author would take on the other end of the scale. Unlike Rudy Rucker's Infinity and the Mind, long the standard popular work on the topic, Barrow spends only about half of the book on the mathematics of infinity. Philosophical, metaphysical, and theological views of the infinite in a variety of cultures are discussed, as well as the history of the infinite in mathematics, including a biographical portrait of the ultimately tragic life of Georg Cantor. The physics of an infinite universe (and whether we can ever determine if our own universe is infinite), the paradoxes of an infinite number of identical copies of ourselves necessarily existing in an infinite universe, the possibility of machines which perform an infinite number of tasks in finite time, whether we're living in a simulation (and how we might discover we are), and the practical and moral consequences of immortality and time travel are also explored.

Mathematicians and scientists have traditionally been very wary of the infinite (indeed, the appearance of infinities is considered an indication of the limitations of theories in modern physics), and Barrow presents any number of paradoxes which illustrate that, as he titles chapter four, “infinity is not a big number”: it is fundamentally different and requires a distinct kind of intuition if nonsensical results are to be avoided. One of the most delightful examples is Zhihong Xia's five-body configuration of point masses which, under Newtonian gravitation, expands to infinite size in finite time. (Don't worry: the finite speed of light, formation of an horizon if two bodies approach too closely, and the emission of gravitational radiation keep this from working in the relativistic universe we inhabit. As the author says [p. 236], “Black holes might seem bad but, like growing old, they are really not so bad when you consider the alternatives.”)

This is an enjoyable and enlightening read, but I found it didn't come up to the standard set by The Book of Nothing and The Constants of Nature (June 2003). Like the latter book, this one is set in a hideously inappropriate font for a work on mathematics: the digit “1” is almost indistinguishable from the letter “I”. If you look very closely at the top serif on the “1” you'll note that it rises toward the right while the “I” has a horizontal top serif. But why go to the trouble of distinguishing the two characters and then making the two glyphs so nearly identical you can't tell them apart without a magnifying glass? In addition, the horizontal bar of the plus sign doesn't line up with the minus sign, which makes equations look awful.

This isn't the author's only work on infinity; he's also written a stage play, Infinities, which was performed in Milan in 2002 and 2003.

September 2007 

Bernstein, Peter L. Against the Gods. New York: John Wiley & Sons, [1996] 1998. ISBN 978-0-471-29563-1.

I do not use the work “masterpiece” lightly, but this is what we have here. What distinguishes the modern epoch from all of the centuries during which humans identical to us trod this Earth? The author, a distinguished and erudite analyst and participant in the securities markets over his long career, argues that one essential invention of the modern era, enabling the vast expansion of economic activity and production of wealth in Western civilisation, is the ability to comprehend, quantify, and ultimately mitigate risk, either by commingling independent risks (as does insurance), or by laying risk off from those who would otherwise bear it onto speculators willing to assume it in the interest of financial gains (for example, futures, options, and other financial derivatives). If, as in the classical world, everyone bears the entire risk of any undertaking, then all market players will be risk-averse for fear of ruin. But if risk can be shared, then the society as a whole will be willing to run more risks, and it is risks voluntarily assumed which ultimately lead (after the inevitable losses) to net gain for all.

So curious and counterintuitive are the notions associated with risk that understanding them took centuries. The ancients, who made such progress in geometry and other difficult fields of mathematics, were, while avid players of games of chance, inclined to attribute the outcome to the will of the Gods. It was not until the Enlightenment that thinkers such as Pascal, Cardano, the many Bernoullis, and others worked out the laws of probability, bringing the inherent randomness of games of chance into a framework which predicted the outcome, not of any given event—that was unknowable in principle, but the result of a large number of plays with arbitrary precision as the number of trials increased. Next was the understanding of the importance of uncertainty in decision making. It's one thing not to know whether a coin will come up heads or tails. It's entirely another to invest in a stock and realise that however accurate your estimation of the probabilistic unknowns affecting its future (for example, the cost of raw materials), it's the “unknown unknowns” (say, overnight bankruptcy due to a rogue trader in an office half way around the world) that can really sink your investment. Finally, classical economics always assumed that participants in the market behave rationally, but they don't. Anybody who thinks their fellow humans are rational need only visit a casino or watch them purchasing lottery tickets; they are sure in the long term to lose, and yet they still line up to make the sucker bet.

Somehow, I'd gotten it into my head that this was a “history of insurance”, and as a result this book sat on my shelf quite some time before I read it. It is much, much more than that. If you have any interest at all in investing, risk management in business ventures, or in the history of probability, statistics, game theory, and investigations of human behaviour in decision making, this is an essential book. Chapter 18 is one of the clearest expositions for its length that I've read of financial derivatives and both the benefits they have for prudent investors as well as the risks they pose to the global financial system. The writing is delightful, and sources are well documented in end notes and an extensive bibliography.

August 2008 

Clawson, Calvin C. Mathematical Mysteries. New York: Perseus Books, 1996. ISBN 978-0-7382-0259-4.

This book might be more accurately titled “Wonders of Number Theory”, but doubtless the publisher feared that would scare away the few remaining customers who weren't intimidated by the many equations in the text. Within that limited scope, and for readers familiar with high school algebra (elementary calculus makes a couple of appearances, but you'll miss little or nothing if you aren't acquainted with it), this is an introduction to the beauty of mathematics, its amazing and unexpected interconnectedness, and the profound intellectual challenge of problems, some posed in ancient Greece, which can easily be explained to a child, yet which remain unsolved after millennia of effort by the most intelligent exemplars of our species.

The hesitant reader is eased into the topic through a variety of easily-comprehended and yet startling results, expanding the concept of number from the natural numbers to the real number line (like calculus, complex numbers only poke their nose under the tent in a few circumstances where they absolutely can't be avoided), and then the author provides a survey of the most profound and intractable puzzles of number theory including the Goldbach conjecture and Riemann hypothesis, concluding with a sketch of Gödel's incompleteness theorems and what it all means.

Two chapters are devoted to the life and work of Ramanujan, using his notebooks to illustrate the beauty of an equation expressing a deep truth and the interconnections in mathematics this singular genius perceived, such as:

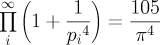
which relates the sequence of prime numbers (p_i is the ith prime number) to the ratio of the circumference to the diameter of a circle. Who could have imagined they had anything to do with one another? And how did 105 get into it?

This book is a pure joy, and a excellent introduction for those who “don't get it” of how mathematics can become a consuming passion for those who do. The only low spot in the book is chapter 9, which discusses the application of large prime numbers to cryptography. While this was much in the news during the crypto wars when the book was published in the mid-1990s, some of the information in this chapter is factually incorrect and misleading, and the attempt at a popular description of the RSA algorithm will probably leave many who actually understand its details scratching their heads. So skip this chapter.

I bought this book shortly after it was published, and it sat on my shelf for a decade and a half until I picked it up and started reading it. I finished it in three days, enjoying it immensely, and I was already familiar with most of the material covered here. For those who are encountering it for the first time, this may be a door into a palace of intellectual pleasures they previously thought to be forbidding, dry, and inaccessible to them.

May 2011 

Dembski, William A. No Free Lunch. Lanham, MD: Rowan & Littlefield, 2002. ISBN 0-7425-1297-5.

It seems to be the rule that the softer the science, the more rigid and vociferously enforced the dogma. Physicists, confident of what they do know and cognisant of how much they still don't, have no problems with speculative theories of parallel universes, wormholes and time machines, and inconstant physical constants. But express the slightest scepticism about Darwinian evolution being the one, completely correct, absolutely established beyond a shadow of a doubt, comprehensive and exclusive explanation for the emergence of complexity and diversity in life on Earth, and outraged biologists run to the courts, the legislature, and the media to suppress the heresy, accusing those who dare to doubt their dogma as being benighted opponents of science seeking to impose a “theocracy”. Funny, I thought science progressed by putting theories to the test, and that all theories were provisional, subject to falsification by experimental evidence or replacement by a more comprehensive theory which explains additional phenomena and/or requires fewer arbitrary assumptions.

In this book, mathematician and philosopher William A. Dembski attempts to lay the mathematical and logical foundation for inferring the presence of intelligent design in biology. Note that “intelligent design” needn't imply divine or supernatural intervention—the “directed panspermia” theory of the origin of life proposed by co-discoverer of the structure of DNA and Nobel Prize winner Francis Crick is a theory of intelligent design which invokes no deity, and my perpetually unfinished work The Rube Goldberg Variations and the science fiction story upon which it is based involve searches for evidence of design in scientific data, not in scripture.

You certainly won't find any theology here. What you will find is logical and mathematical arguments which sometimes ascend (or descend, if you wish) into prose like (p. 153), “Thus, if P characterizes the probability of E₀ occurring and f characterizes the physical process that led from E₀ to E₁, then P∘f ⁻¹ characterizes the probability of E₁ occurring and P(E₀) ≤ P∘f ⁻¹(E₁) since f(E₀) = E₁ and thus E₀ ⊂ f ⁻¹(E₁).” OK, I did cherry-pick that sentence from a particularly technical section which the author advises readers to skip if they're willing to accept the less formal argument already presented. Technical arguments are well-supplemented by analogies and examples throughout the text.

Dembski argues that what he terms “complex specified information” is conclusive evidence for the presence of design. Complexity (the Shannon information measure) is insufficient—all possible outcomes of flipping a coin 100 times in a row are equally probable—but presented with a sequence of all heads, all tails, alternating heads and tails, or a pattern in which heads occurred only for prime numbered flips, the evidence for design (in this case, cheating or an unfair coin) would be considered overwhelming. Complex information is considered specified if it is compressible in the sense of Chaitin-Kolmogorov-Solomonoff algorithmic information theory, which measures the randomness of a bit string by the length of the shortest computer program which could produce it. The overwhelming majority of 100 bit strings cannot be expressed more compactly than simply by listing the bits; the examples given above, however, are all highly compressible. This is the kind of measure, albeit not rigorously computed, which SETI researchers would use to identify a signal as of intelligent origin, which courts apply in intellectual property cases to decide whether similarity is accidental or deliberate copying, and archaeologists use to determine whether an artefact is of natural or human origin. Only when one starts asking these kinds of questions about biology and the origin of life does controversy erupt!

Chapter 3 proposes a “Law of Conservation of Information” which, if you accept it, would appear to rule out the generation of additional complex specified information by the process of Darwinian evolution. This would mean that while evolution can and does account for the development of resistance to antibiotics in bacteria and pesticides in insects, modification of colouration and pattern due to changes in environment, and all the other well-confirmed cases of the Darwinian mechanism, that innovation of entirely novel and irreducibly complex (see chapter 5) mechanisms such as the bacterial flagellum require some external input of the complex specified information they embody. Well, maybe…but one should remember that conservation laws in science, unlike invariants in mathematics, are empirical observations which can be falsified by a single counter-example. Niels Bohr, for example, prior to its explanation due to the neutrino, theorised that the energy spectrum of nuclear beta decay could be due to a violation of conservation of energy, and his theory was taken seriously until ruled out by experiment.

Let's suppose, for the sake of argument, that Darwinian evolution does explain the emergence of all the complexity of the Earth's biosphere, starting with a single primordial replicating lifeform. Then one still must explain how that replicator came to be in the first place (since Darwinian evolution cannot work on non-replicating organisms), and where the information embodied in its molecular structure came from. The smallest present-day bacterial genomes belong to symbiotic or parasitic species, and are in the neighbourhood of 500,000 base pairs, or roughly 1 megabit of information. Even granting that the ancestral organism might have been much smaller and simpler, it is difficult to imagine a replicator capable of Darwinian evolution with an information content 1000 times smaller than these bacteria, Yet randomly assembling even 500 bits of precisely specified information seems to be beyond the capacity of the universe we inhabit. If you imagine every one of the approximately 10⁸⁰ elementary particles in the universe trying combinations every Planck interval, 10⁴⁵ times every second, it would still take about a billion times the present age of the universe to randomly discover a 500 bit pattern. Of course, there are doubtless many patterns which would work, but when you consider how conservative all the assumptions are which go into this estimate, and reflect upon the evidence that life seemed to appear on Earth just about as early as environmental conditions permitted it to exist, it's pretty clear that glib claims that evolution explains everything and there are just a few details to be sorted out are arm-waving at best and propaganda at worst, and that it's far too early to exclude any plausible theory which could explain the mystery of the origin of life. Although there are many points in this book with which you may take issue, and it does not claim in any way to provide answers, it is valuable in understanding just how difficult the problem is and how many holes exist in other, more accepted, explanations. A clear challenge posed to purely naturalistic explanations of the origin of terrestrial life is to suggest a prebiotic mechanism which can assemble adequate specified information (say, 500 bits as the absolute minimum) to serve as a primordial replicator from the materials available on the early Earth in the time between the final catastrophic bombardment and the first evidence for early life.

May 2005 

Derbyshire, John. Prime Obsession. Washington: Joseph Henry Press, 2003. ISBN 0-309-08549-7.

This is simply the finest popular mathematics book I have ever read.

June 2003 

Derbyshire, John. Unknown Quantity. Washington: Joseph Henry Press, 2006. ISBN 0-309-09657-X.

After exploring a renowned mathematical conundrum (the Riemann Hypothesis) in all its profundity in Prime Obsession (June 2003), in this book the author recounts the history of algebra—an intellectual quest sprawling over most of recorded human history and occupying some of the greatest minds our species has produced. Babylonian cuneiform tablets dating from the time of Hammurabi, about 3800 years ago, demonstrate solving quadratic equations, extracting square roots, and finding Pythagorean triples. (The methods in the Babylonian texts are recognisably algebraic but are expressed as “word problems” instead of algebraic notation.) Diophantus, about 2000 years later, was the first to write equations in a symbolic form, but this was promptly forgotten. In fact, twenty-six centuries after the Babylonians were solving quadratic equations expressed in word problems, al-Khwārizmī (the word “algebra” is derived from the title of his book, الكتاب المختصر في حساب الجبر والمقابلة
al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala, and “algorithm” from his name) was solving quadratic equations in word problems. It wasn't until around 1600 that anything resembling the literal symbolism of modern algebra came into use, and it took an intellect of the calibre of René Descartes to perfect it. Finally, equipped with an expressive notation, rules for symbolic manipulation, and the slowly dawning realisation that this, not numbers or geometric figures, is ultimately what mathematics is about, mathematicians embarked on a spiral of abstraction, discovery, and generalisation which has never ceased to accelerate in the centuries since. As more and more mathematics was discovered (or, if you're an anti-Platonist, invented), deep and unexpected connections were found among topics once considered unrelated, and this is a large part of the story told here, as algebra has “infiltrated” geometry, topology, number theory, and a host of other mathematical fields while, in the form of algebraic geometry and group theory, providing the foundation upon which the most fundamental theories of modern physics are built.

With all of these connections, there's a strong temptation for an author to wander off into fields not generally considered part of algebra (for example, analysis or set theory); Derbyshire is admirable in his ability to stay on topic, while not shortchanging the reader where important cross-overs occur. In a book of this kind, especially one covering such a long span of history and a topic so broad, it is difficult to strike the right balance between explaining the mathematics and sketching the lives of the people who did it, and between a historical narrative and one which follows the evolution of specific ideas over time. In the opinion of this reader, Derbyshire's judgement on these matters is impeccable. As implausible as it may seem to some that a book about algebra could aspire to such a distinction, I found this one of the more compelling page-turners I've read in recent months.

Six “math primers” interspersed in the text provide the fundamentals the reader needs to understand the chapters which follow. While excellent refreshers, readers who have never encountered these concepts before may find the primers difficult to comprehend (but then, they probably won't be reading a history of algebra in the first place). Thirty pages of end notes not only cite sources but expand, sometimes at substantial length, upon the main text; readers should not deprive themselves this valuable lagniappe.

January 2007 

Gamow, George. One, Two, Three…Infinity. Mineola, NY: Dover, [1947] 1961. rev. ed. ISBN 0-486-25664-2.

This book, which first I read at around age twelve, rekindled my native interest in mathematics and science which had, by then, been almost entirely extinguished by six years of that intellectual torture called “classroom instruction”. Gamow was an eminent physicist: among other things, he advocated the big bang theory decades before it became fashionable, originated the concept of big bang nucleosynthesis, predicted the cosmic microwave background radiation 16 years before it was discovered, proposed the liquid drop model of the atomic nucleus, worked extensively in the astrophysics of energy production in stars, and even designed a nuclear bomb (“Greenhouse George”), which initiated the first deuterium-tritium fusion reaction here on Earth. But he was also one of most talented popularisers of science in the twentieth century, with a total of 18 popular science books published between 1939 and 1967, including the Mr Tompkins series, timeless classics which inspired many of the science visualisation projects at this site, in particular C-ship. A talented cartoonist as well, 128 of his delightful pen and ink drawings grace this volume. For a work published in 1947 with relatively minor revisions in the 1961 edition, this book has withstood the test of time remarkably well—Gamow was both wise and lucky in his choice of topics. Certainly, nobody should consider this book a survey of present-day science, but for folks well-grounded in contemporary orthodoxy, it's a delightful period piece providing a glimpse of the scientific world view of almost a half-century ago as explained by a master of the art. This Dover paperback is an unabridged reprint of the 1961 revised edition.

September 2004 

Gleick, James. Isaac Newton. New York: Pantheon Books, 2003. ISBN 0-375-42233-1.

Fitting a satisfying biography of one of the most towering figures in the history of the human intellect into fewer than 200 pages is a formidable undertaking, which James Gleick has accomplished magnificently here. Newton's mathematics and science are well covered, placing each in the context of the “shoulders of Giants” which he said helped him see further, but also his extensive (and little known, prior to the twentieth century) investigations into alchemy, theology, and ancient history. His battles with Hooke, Leibniz, and Flamsteed, autocratic later years as Master of the Royal Mint and President of the Royal Society and ceaseless curiosity and investigation are well covered, as well as his eccentricity and secretiveness. I'm a little dubious of the discussion on pp. 186–187 where Newton is argued to have anticipated or at least left the door open for relativity, quantum theory, equivalence of mass and energy, and subatomic forces. Newton wrote millions of words on almost every topic imaginable, most for his own use with no intention of publication, few examined by scholars until centuries after his death. From such a body of text, it may be possible to find sentences here and there which “anticipate” almost anything when you know from hindsight what you're looking for. In any case, the achievements of Newton, who not only laid the foundation of modern physical science, invented the mathematics upon which much of it is based, and created the very way we think about and do science, need no embellishment. The text is accompanied by 48 pages of endnotes (the majority citing primary sources) and an 18 page bibliography. A paperback edition is now available.

November 2004 

Gray, Jeremy J. The Hilbert Challenge. Oxford: Oxford University Press, 2000. ISBN 0-19-850651-1.

August 2001 

Guy, Richard K. Unsolved Problems in Number Theory. 3rd ed. New York: Springer, 2004. ISBN 0-387-20860-7.

Your hard-working and overheated CPU chip does not want you to buy this book! Collected here are hundreds of thorny problems, puzzles, and conjectures, many of which, even if you lack the cerebral horsepower to tackle a formal proof, are candidates for computational searches for solutions or counterexamples (and, indeed, a substantial number of problems posed in the first and second editions have been so resolved, some with quite modest computation by today's standards). In the 18th century, Leonhard Euler conjectured that there was no nontrivial solution to the equation: a⁵ + b⁵ + c⁵ + d⁵ = e⁵ The problem remained open until 1966 when Lander and Parkin found the counterexample: 27⁵ + 84⁵ + 110⁵ + 133⁵ = 144⁵ Does the equation: a⁶ + b⁶ + c⁶ + d⁶ + e⁶ = f⁶ have a nontrivial integer solution? Ladies and gentlemen, start your (analytical) engines! (Problem D1.) There are a large collection of mathematical curiosities here, including a series which grows so slowly it is proportional to the inverse of the Ackermann function (E20), and a conjecture (E16) regarding the esoteric equation “3x+1” about which Paul Erdös said, “Mathematics may not be ready for such problems.” The 196 palindrome problem which caused me to burn up three years of computer time some fifteen years ago closes the book (F32). Many (but not all) of the problems to which computer attacks are applicable indicate the status of searches as of 2003, giving you some idea what you're getting into should you be inclined to launch your own.

For a book devoted to one of the most finicky topics in pure mathematics, there are a dismaying number of typographical errors, and not just in the descriptive text. Even some of the LaTeX macros used to typeset the book are bungled, with “@”-form \index entries appearing explicitly in the text. Many of the errors would have been caught by a spelling checker, and there are a number of rather obvious typesetting errors in equations. As the book contains an abundance of “magic numbers” related to the various problems which may figure in computer searches, I would make a point to independently confirm their accuracy before launching any extensive computing project.

September 2005 

Havil, Julian. Gamma: Exploring Euler's Constant. Princeton: Princeton University Press, 2003. ISBN 0-691-09983-9.

September 2003 

Hellman, Hal. Great Feuds in Mathematics. Hoboken, NJ: John Wiley & Sons, 2006. ISBN 0-471-64877-9.

Since antiquity, many philosophers have looked upon mathematics as one thing, perhaps the only thing, that we can know for sure, “the last fortress of certitude” (p. 200). Certainly then, mathematicians must be dispassionate explorers of this frontier of knowledge, and mathematical research a grand collaborative endeavour, building upon the work of the past and weaving the various threads of inquiry into a seamless intellectual fabric. Well, not exactly….

Mathematicians are human, and mathematical research is a human activity like any other, so regardless of the austere crystalline perfection of the final product, the process of getting there can be as messy, contentious, and consequently entertaining as any other enterprise undertaken by talking apes. This book chronicles ten of the most significant and savage disputes in the history of mathematics. The bones of contention vary from the tried-and-true question of priority (Tartaglia vs. Cardano on the solution to cubic polynomials, Newton vs. Leibniz on the origin of the differential and integral calculus), the relation of mathematics to the physical sciences (Sylvester vs. Huxley), the legitimacy of the infinite in mathematics (Kronecker vs. Cantor, Borel vs. Zermelo), the proper foundation for mathematics (Poincaré vs. Russell, Hilbert vs. Brouwer), and even sibling rivalry (Jakob vs. Johann Bernoulli). A final chapter recounts the incessantly disputed question of whether mathematicians discover structures that are “out there” (as John D. Barrow puts it, “Pi in the Sky”) or invent what is ultimately as much a human construct as music or literature.

The focus is primarily on people and events, less so on the mathematical questions behind the conflict; if you're unfamiliar with the issues involved, you may want to look them up in other references. The stories presented here are an excellent antidote to the retrospective view of many accounts which present mathematical history as a steady march forward, with each generation building upon the work of the previous. The reality is much more messy, with the directions of inquiry chosen for reasons of ego and national pride as often as inherent merit, and the paths not taken often as interesting as those which were. Even if you believe (as I do) that mathematics is “out there”, the human struggle to discover and figure out how it all fits together is interesting and ultimately inspiring, and this book provides a glimpse into that ongoing quest.

December 2007 

Holt, John. How Children Fail. rev. ed. Cambridge, MA: Da Capo Press, [1964] 1982. ISBN 0-201-48402-1.

This revised edition of Holt's classic includes the entire text of the 1964 first edition with extensive additional interspersed comments added after almost twenty years of additional experience and reflection. It is difficult to find a book with as much wisdom and as many insights per page as this one. You will be flabbergasted by Holt's forensic investigation of how many fifth graders (in an elite private school for high IQ children) actually think about arithmetic, and how many teachers and parents delude themselves into believing that parroting correct answers has anything to do with understanding or genuine learning. What is so refreshing about Holt is his scientific approach—he eschews theory and dogma in favour of observing what actually goes on in classrooms and inside the heads of students. Some of his insights about how those cunning little rascals game the system to get the right answer without enduring the submission to authority and endless boredom of what passes for education summoned some of the rare fond memories I have of that odious period in my own life. As a person who's spent a lot of time recently thinking about intelligence, problem solving, and learning, I found Holt's insights absolutely fascinating. This book has sold more than a million copies, but I'd have probably never picked it up had it not been recommended by a kind reader using the recommendation form—thank you!

September 2004 

Maor, Eli. e: The Story of a Number. Princeton: Princeton University Press, [1994] 1998. ISBN 0-691-05854-7.

February 2002 

Mashaal, Maurice. Bourbaki: A Secret Society of Mathematicians. Translated by Anna Pierrehumbert. Providence, RI: American Mathematical Society, [2002] 2006. ISBN 978-0-8218-3967-6.

In 1934, André Weil and Henri Cartan, both young professors of mathematics at the University of Strasbourg, would frequently, when discussing the calculus courses they were teaching, deplore the textbooks available, all of which they considered antiquated and inadequate. Weil eventually suggested getting in touch with several of their fellow alumni of the École Normale Supérieure who were teaching similar courses in provincial universities around France, inviting them to collaborate on a new analysis textbook. The complete work was expected to total 1000 to 1200 pages, with the first volumes ready about six months after the project began.

Thus began one of the most flabbergasting examples of “mission creep” in human intellectual history, which set the style for much of mathematics publication and education in subsequent decades. Working collectively and publishing under the pseudonym “Nicolas Bourbaki” (after the French general in the Franco-Prussian War Charles Denis Bourbaki), the “analysis textbook” to be assembled by a small group over a few years grew into a project spanning more than six decades and ten books, most of multiple volumes, totalling more than seven thousand pages, systematising the core of mathematics in a relentlessly abstract and austere axiomatic form. Although Bourbaki introduced new terminology, some of which has become commonplace, there is no new mathematics in the work: it is a presentation of pre-existing mathematical work as a pedagogical tool and toolbox for research mathematicians. (This is not to say that the participants in the Bourbaki project did not do original work—in fact, they were among the leaders in mathematical research in their respective generations. But their work on the Bourbaki opus was a codification and grand unification of the disparate branches of mathematics into a coherent whole. In fact, so important was the idea that mathematics was a unified tree rooted in set theory that the Bourbaki group always used the word mathématique, not mathématiques.)

Criticisms of the Bourbaki approach were many: it was too abstract, emphasised structure over the content which motivated it, neglected foundational topics such as mathematical logic, excluded anything tainted with the possibility of application (including probability, automata theory, and combinatorics), and took an eccentric approach to integration, disdaining the Lebesgue integral. These criticisms are described in detail, with both sides fairly presented. While Bourbaki participants had no ambitions to reform secondary school mathematics education, it is certainly true that academics steeped in the Bourbaki approach played a part in the disastrous “New Math” episode, which is described in chapter 10.

The book is extravagantly illustrated, and has numerous boxes and marginal notes which describe details, concepts, and the dramatis personæ in this intricate story. An appendix provides English translations of documents which appear in French in the main text. There is no index.

La version française reste disponible.

January 2008 

Mazur, Joseph. Enlightening Symbols. Princeton: Princeton University Press, 2014. ISBN 978-0-691-15463-3.

Sometimes an invention is so profound and significant yet apparently obvious in retrospect that it is difficult to imagine how people around the world struggled over millennia to discover it, and how slowly it was to diffuse from its points of origin into general use. Such is the case for our modern decimal system of positional notation for numbers and the notation for algebra and other fields of mathematics which permits rapid calculation and transformation of expressions. This book, written with the extensive source citations of a scholarly work yet accessible to any reader familiar with arithmetic and basic algebra, traces the often murky origins of this essential part of our intellectual heritage.

From prehistoric times humans have had the need to count things, for example, the number of sheep in a field. This could be done by establishing a one-to-one correspondence between the sheep and something else more portable such as one's fingers (for a small flock), or pebbles kept in a sack. To determine whether a sheep was missing, just remove a pebble for each sheep and if any remained in the sack, that indicates how many are absent. At a slightly more abstract level, one could make tally marks on a piece of bark or clay tablet, one for each sheep. But all of this does not imply number as an abstraction independent of individual items of some kind or another. Ancestral humans don't seem to have required more than the simplest notion of numbers: until the middle of the 20th century several tribes of Australian aborigines had no words for numbers in their languages at all, but counted things by making marks in the sand. Anthropologists discovered tribes in remote areas of the Americas, Pacific Islands, and Australia whose languages had no words for numbers greater than four.

With the emergence of settled human populations and the increasingly complex interactions of trade between villages and eventually cities, a more sophisticated notion of numbers was required. A merchant might need to compute how many kinds of one good to exchange for another and to keep records of his inventory of various items. The earliest known written records of numerical writing are Sumerian cuneiform clay tablets dating from around 3400 B.C. These tablets show number symbols formed from two distinct kinds of marks pressed into wet clay with a stylus. While the smaller numbers seem clearly evolved from tally marks, larger numbers are formed by complicated combinations of the two symbols representing numbers from 1 to 59. Larger numbers were written as groups of powers of 60 separated by spaces. This was the first known instance of a positional number system, but there is no evidence it was used for complicated calculations—just as a means of recording quantities.

Ancient civilisations: Egypt, Hebrew, Greece, China, Rome, and the Aztecs and Mayas in the Western Hemisphere all invented ways of writing numbers, some sophisticated and capable of representing large quantities. Many of these systems were additive: they used symbols, sometimes derived from letters in their alphabets, and composed numbers by writing symbols which summed to the total. To write the number 563, a Greek would write “φξγ”, where φ=500, ξ=60, and γ=3. By convention, numbers were written with letters in descending order of the value they represented, but the system was not positional. This made the system clumsy for representing large numbers, reusing letters with accent marks to represent thousands and an entirely different convention for ten thousands.

How did such advanced civilisations get along using number systems in which it is almost impossible to compute? Just imagine a Roman faced with multiplying MDXLIX by XLVII (1549 × 47)—where do you start? You don't: all of these civilisations used some form of mechanical computational aid: an abacus, counting rods, stones in grooves, and so on to actually manipulate numbers. The Sun Zi Suan Jing, dating from fifth century China, provides instructions (algorithms) for multiplication, division, and square and cube root extraction using bamboo counting sticks (or written symbols representing them). The result of the computation was then written using the numerals of the language. The written language was thus a way to represent numbers, but not compute with them.

Many of the various forms of numbers and especially computational tools such as the abacus came ever-so-close to stumbling on the place value system, but it was in India, probably before the third century B.C. that a positional decimal number system including zero as a place holder, with digit forms recognisably ancestral to those we use today emerged. This was a breakthrough in two regards. Now, by memorising tables of addition, subtraction, multiplication, and division and simple algorithms once learned by schoolchildren before calculators supplanted that part of their brains, it was possible to directly compute from written numbers. (Despite this, the abacus remained in common use.) But, more profoundly, this was a universal representation of whole numbers. Earlier number systems (with the possible exception of that invented by Archimedes in The Sand Reckoner [but never used practically]) either had a limit on the largest number they could represent or required cumbersome and/or lengthy conventions for large numbers. The Indian number system needed only ten symbols to represent any non-negative number, and only the single convention that each digit in a number represented how many of that power of ten depending on its position.

Knowledge diffused slowly in antiquity, and despite India being on active trade routes, it was not until the 13th century A.D. that Fibonacci introduced the new number system, which had been transmitted via Islamic scholars writing in Arabic, to Europe in his Liber Abaci. This book not only introduced the new number system, it provided instructions for a variety of practical computations and applications to higher mathematics. As revolutionary as this book was, in an era of hand-copied manuscripts, its influence spread very slowly, and it was not until the 16th century that the new numbers became almost universally used. The author describes this protracted process, about which a great deal of controversy remains to the present day.

Just as the decimal positional number system was becoming established in Europe, another revolution in notation began which would transform mathematics, how it was done, and our understanding of the meaning of numbers. Algebra, as we now understand it, was known in antiquity, but it was expressed in a rhetorical way—in words. For example, proposition 7 of book 2 of Euclid's Elements states:

If a straight line be cut at random, the square of the whole is equal to the squares on the segments and twice the rectangle contained by the segments.

Now, given such a problem, Euclid or any of those following in his tradition would draw a diagram and proceed to prove from the axioms of plane geometry the correctness of the statement. But it isn't obvious how to apply this identity to other problems, or how it illustrates the behaviour of general numbers. Today, we'd express the problem and proceed as follows:

Once again, faced with the word problem, it's difficult to know where to begin, but once expressed in symbolic form, it can be solved by applying rules of algebra which many master before reaching high school. Indeed, the process of simplifying such an equation is so mechanical that computer tools are readily available to do so.

Or consider the following brain-twister posed in the 7th century A.D. about the Greek mathematician and father of algebra Diophantus: how many years did he live?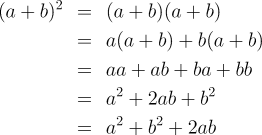

“Here lies Diophantus,” the wonder behold.
Through art algebraic, the stone tells how old;
“God gave him his boyhood one-sixth of his life,
One twelfth more as youth while whiskers grew rife;
And then one-seventh ere marriage begun;
In five years there came a bounding new son.
Alas, the dear child of master and sage
After attaining half the measure of his father's life chill fate took him.
After consoling his fate by the science of numbers for four years, he ended his life.”

Oh, go ahead, give it a try before reading on!

Today, we'd read through the problem and write a system of two simultaneous equations, where x is the age of Diophantus at his death and y the number of years his son lived. Then:

Plug the second equation into the first, do a little algebraic symbol twiddling, and the answer, 84, pops right out. Note that not only are the rules for solving this equation the same as for any other, with a little practice it is easy to read the word problem and write down the equations ready to solve. Go back and re-read the original problem and the equations and you'll see how straightforwardly they follow.

Once you have transformed a mass of words into symbols, they invite you to discover new ways in which they apply. What is the solution of the equation x+4=0? In antiquity many would have said the equation is meaningless: there is no number you can add to four to get zero. But that's because their conception of number was too limited: negative numbers such as −4 are completely valid and obey all the laws of algebra. By admitting them, we discovered we'd overlooked half of the real numbers. What about the solution to the equation x² + 4 = 0? This was again considered ill-formed, or imaginary, since the square of any real number, positive or negative, is positive. Another leap of imagination, admitting the square root of minus one to the family of numbers, expanded the number line into the complex plane, yielding the answer 2i as we'd now express it, and extending our concept of number into one which is now fundamental not only in abstract mathematics but also science and engineering. And in recognising negative and complex numbers, we'd come closer to unifying algebra and geometry by bringing rotation into the family of numbers.

This book explores the groping over centuries toward a symbolic representation of mathematics which hid the specifics while revealing the commonality underlying them. As one who learned mathematics during the height of the “new math” craze, I can't recall a time when I didn't think of mathematics as a game of symbolic transformation of expressions which may or may not have any connection with the real world. But what one discovers in reading this book is that while this is a concept very easy to brainwash into a 7th grader, it was extraordinarily difficult for even some of the most brilliant humans ever to have lived to grasp in the first place. When Newton invented calculus, for example, he always expressed his “fluxions” as derivatives of time, and did not write of the general derivative of a function of arbitrary variables.

Also, notation is important. Writing something in a more expressive and easily manipulated way can reveal new insights about it. We benefit not just from the discoveries of those in the past, but from those who created the symbolic language in which we now express them.

This book is a treasure chest of information about how the language of science came to be. We encounter a host of characters along the way, not just great mathematicians and scientists, but scoundrels, master forgers, chauvinists, those who preserved precious manuscripts and those who burned them, all leading to the symbolic language in which we so effortlessly write and do mathematics today.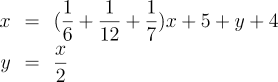

January 2015 

Netz, Reviel and William Noel. The Archimedes Codex. New York: Da Capo Press, 2007. ISBN 978-0-306-81580-5.

Sometimes it is easy to forget just how scanty is the material from which we know the origins of Western civilisation. Archimedes was one of the singular intellects of antiquity, with contributions to mathematics, science, and engineering which foreshadowed achievements not surpassed until the Enlightenment. And yet all we know of the work of Archimedes in the original Greek (as opposed to translations into Arabic and Latin, which may have lost information due to translators' lack of comprehension of Archimedes's complex arguments) can be traced to three manuscripts: one which disappeared in 1311, another which vanished in the 1550s, and a third: the Archimedes Palimpsest, which surfaced in Constantinople at the start of the 20th century, and was purchased at an auction for more than USD 2 million by an anonymous buyer who deposited it for conservation and research with the Walters Art Museum in Baltimore. (Note that none of these manuscripts was the original work of Archimedes: all were copies made by scribes, probably around the tenth century. But despite being copies, their being in the original Greek means they are far more likely to preserve the sense of the original text of Archimedes, even if the scribe did not understand what he was copying.)

History has not been kind to this work of Archimedes. Only two centuries after the copy of his work was made, the parchment on which it was written was scrubbed of its original content and re-written with the text of a Christian prayer book, which to the unaided eye appears to completely obscure the Archimedes text in much of the work. To compound the insult, sometime in the 20th century four full-page religious images in Byzantine style were forged over pages of the book, apparently in an attempt to increase its market value. This, then, was a bogus illustration painted on top of the prayer book text, which was written on top of the precious words of Archimedes. In addition to these depredations of mankind, many pages had been attacked by mold, and an ill-advised attempt to conserve the text, apparently in the 1960s, had gummed up the binding, including the gutter of the page where Archimedes's text was less obscured, with an intractable rubbery glue.

But from what could be read, even in fragments, it was clear that the text, if it could be extracted, would be of great significance. Two works, “The Method” and “Stomachion”, have their only known copies in this text, and the only known Greek text of “On Floating Bodies” appears here as well. Fortunately, the attempt to extract the Archimedes text was made in the age of hyperspectral imaging, X-ray fluorescence, and other nondestructive technologies, not with the crude and often disastrous chemical potions applied to attempt to recover such texts a century before.

This book, with alternating chapters written by the curator of manuscripts at the Walters and a Stanford professor of Classics and Archimedes scholar, tells the story of the origin of the manuscript, how it came to be what it is and where it resides today, and the painstaking efforts at conservation and technological wizardry (including time on the synchrotron light source beamline at SLAC) which allowed teasing the work of Archimedes from the obscuration of centuries.

What has been found so far has elevated the reputation of Archimedes even above the exalted position he already occupied in the pantheon of science. Analysis of “The Method” shows that Archimedes anticipated the use of infinitesimals and hence the calculus in his proof of the volume of curved solids. The “Stomachion”, originally thought to be a puzzle devoid of serious mathematical interest, turns out to be the first and only known venture of Greek mathematics into the realm of combinatorics.

If you're interested in rare books, the origins of mathematical thought, applications of imaging technology to historical documents, and the perilous path the words of the ancients traverse to reach us across the ages, there is much to fascinate in this account. Special thanks to frequent recommender of books Joe Marasco, who not only brought this book to my attention but mailed me a copy! Joe played a role in the discovery of the importance of the “Stomachion”, which is chronicled in the chapter “Archimedes at Play”.

August 2008 

Paulos, John Allen. A Mathematician Plays The Stock Market. New York: Basic Books, 2003. ISBN 0-465-05481-1.

Paulos, a mathematics professor and author of several popular books including Innumeracy and A Mathematician Reads the Newspaper, managed to lose a painfully large pile of money (he never says how much) in Worldcom (WCOM) stock in 2000–2002. Other than broadly-based index funds, this was Paulos's first flier in the stock market, and he committed just about every clueless market-newbie blunder in the encyclopedia of Wall Street woe: he bought near the top, on margin, met every margin call and “averaged down” all the way from $47 to below $5 per share, bought out-of-the-money call options on a stock in a multi-year downtrend, never placed stop loss orders or hedged with put options or shorting against the box, based his decisions selectively on positive comments in Internet chat rooms, and utterly failed to diversify (liquidating index funds to further concentrate in a single declining stock). This book came highly recommended, but I found it unsatisfying. Paulos uses his experience in the market as a leitmotif in a wide ranging but rather shallow survey of the mathematics and psychology of markets and investors. Along the way we encounter technical and fundamental analysis, the efficient market hypothesis, compound interest and exponential growth, algorithmic complexity, nonlinear functions and fractals, modern portfolio theory, game theory and the prisoner's dilemma, power laws, financial derivatives, and a variety of card tricks, psychological games, puzzles, and social and economic commentary. Now all of this adds up to only 202 pages, so nothing is treated in much detail—while the explanation of compound interest is almost tedious, many of the deeper mathematical concepts may not be explained sufficiently for readers who don't already understand them. The “leitmotif” becomes pretty heavy after the fiftieth time or so the author whacks himself over the head for his foolishness, and wastes a lot of space which would have been better used discussing the market in greater depth. He dismisses technical analysis purely on the basis of Elliott wave theory, without ever discussing the psychological foundation of many chart patterns as explained in Edwards and Magee; the chapter on fundamental analysis mentions Graham and Dodd only in passing. The author's incessant rambling and short attention span leaves you feeling like you do after a long conversation with Ted Nelson. There is interesting material here, and few if any serious errors, but the result is kind of like English cooking—there's nothing wrong with the ingredients; it's what's done with them that's ultimately bland and distasteful.

September 2004 

Pickover, Clifford A. Surfing through Hyperspace. Oxford: Oxford University Press, 1999. ISBN 0-19-514241-1.

October 2001 

Pickover, Clifford A. The Loom of God. New York: Perseus Books, 1997. ISBN 0-306-45411-4.

Clifford Pickover has more than enough imagination for a hundred regular people. An enormously prolific author, his work includes technical books on computing and scientific visualisation, science fiction, and popular works on mathematics and a wide variety of scientific topics. This book explores the boundary between mathematics and religion, including Pythagorean cults, Stonehenge, cave paintings from 20,000 years ago which may be the first numbers, the Kabala, the quipu of the Incas, numerology, eschatology, and real-world doomsday scenarios, along with a wide variety of puzzles in number theory, geometry, and other mathematical topics. One of the many fascinating unsolved problems he discusses is the “integer brick”, which seems to be more often referred to as the “perfect cuboid”: can you find a three-dimensional rectangular parallelopiped in which all the edges and face and space diagonals are integers? Computer searches have shown than no cuboid with a smallest edge less than 1,281,000,000 satisfies this requirement but, who knows, you may find it in just a few more compute cycles! (I'll pass on this one, after spending three years of computer time pursuing another unicorn of recreational mathematics.) As with Pickover's other popular books, this one includes source code for programs to explore topics raised in the text, explanation of the science and history behind the science fiction narrative, and extensive literature citations for those interested in digging deeper.

March 2005 

Roberts, Siobhan. King of Infinite Space. New York: Walker and Company, 2006. ISBN 0-8027-1499-4.

Mathematics is often said to be a game for the young. The Fields Medal, the most prestigious prize in mathematics, is restricted to candidates 40 years or younger. While many older mathematicians continue to make important contributions in writing books, teaching, administration, and organising and systematising topics, most work on the cutting edge is done by those in their twenties and thirties. The life and career of Donald Coxeter (1907–2003), the subject of this superb biography, is a stunning and inspiring counter-example. Coxeter's publications (all of which are listed in an appendix to this book) span a period of eighty years, with the last, a novel proof of Beecroft's theorem, completed just a few days before his death.

Coxeter was one of the last generation to be trained in classical geometry, and he continued to do original work and make striking discoveries in that field for decades after most other mathematicians had abandoned it as mined out or insufficiently rigorous, and it had disappeared from the curriculum not only at the university level but, to a great extent, in secondary schools as well. Coxeter worked in an intuitive, visual style, frequently making models, kaleidoscopes, and enriching his publications with numerous diagrams. Over the many decades his career spanned, mathematical research (at least in the West) seemed to be climbing an endless stairway toward ever greater abstraction and formalism, epitomised in the work of the Bourbaki group. (When the unthinkable happened and a diagram was included in a Bourbaki book, fittingly it was a Coxeter diagram.) Coxeter inspired an increasingly fervent group of followers who preferred to discover new structures and symmetry using the mind's powers of visualisation. Some, including Douglas Hofstadter (who contributed the foreword to this work) and John Horton Conway (who figures prominently in the text) were inspired by Coxeter to carry on his legacy. Coxeter's interactions with M. C. Escher and Buckminster Fuller are explored in two chapters, and illustrate how the purest of mathematics can both inspire and be enriched by art and architecture (or whatever it was that Fuller did, which Coxeter himself wasn't too sure about—on one occasion he walked out of a new-agey Fuller lecture, noting in his diary “Out, disgusted, after ¾ hour” [p. 178]).

When the “new math” craze took hold in the 1960s, Coxeter immediately saw it for the disaster it was to be become and involved himself in efforts to preserve the intuitive and visual in mathematics education. Unfortunately, the power of a fad promoted by purists is difficult to counter, and a generation and more paid the price of which Coxeter warned. There is an excellent discussion at the end of chapter 9 of the interplay between the intuitive and formalist approaches to mathematics. Many modern mathematicians seem to have forgotten that one proves theorems in order to demonstrate that the insights obtained by intuition are correct. Intuition without rigour can lead to error, but rigour without intuition can blind one to beautiful discoveries in the mathematical objects which stand behind the austere symbols on paper.

The main text of this 400 page book is only 257 pages. Eight appendices expand upon technical topics ranging from phyllotaxis to the quilting of toilet paper and include a complete bibliography of Coxeter's publications. (If you're intrigued by “Morley's Miracle”, a novel discovery in the plane geometry of triangles made as late as 1899, check out this page and Java applet which lets you play with it interactively. Curiously, a diagram of Morley's theorem appears on the cover of Coxeter's and Greitzer's Geometry Revisited, but is misdrawn—the trisectors are inexact and the inner triangle is therefore not equilateral.) Almost 90 pages of endnotes provide both source citations (including Web links to MathWorld for technical terms and the University of St. Andrews biographical archive for mathematicians named in the text) and detailed amplification of numerous details. There are a few typos and factual errors (for example, on p. 101 the planets Uranus and Pluto are said to have been discovered in the nineteenth century when, in fact, neither was: Herschel discovered Uranus in 1781 and Tombaugh Pluto in 1930), but none are central to the topic nor detract from this rewarding biography of an admirable and important mathematician.

February 2007 

Ronan, Mark. Symmetry and the Monster. Oxford: Oxford University Press, 2006. ISBN 0-19-280722-6.

On the morning of May 30th, 1832, self-taught mathematical genius and revolutionary firebrand Évariste Galois died in a duel in Paris, the reasons for which are forgotten; he was twenty years old. The night before, he wrote a letter in which he urged that his uncompleted mathematical work be sent to the preeminent contemporary mathematicians Jacobi and Gauss; neither, however, ever saw it. The work in question laid the foundations for group theory, an active area of mathematical research a century and three quarters hence, and a cornerstone of the most fundamental theories of physics: Noether's Theorem demonstrates that conservation laws and physical symmetries are two aspects of the same thing.

Finite groups, which govern symmetries among a finite number of discrete items (as opposed to, say, the rotations of a sphere, which are continuously valued), can be arbitrarily complicated, but, as shown by Galois, can be decomposed into one or more simple groups whose only normal subgroups are the trivial subgroup of order one and the improper subgroup consisting of the entire group itself: these are the fundamental kinds of symmetries or, as this book refers to them, the “atoms of symmetry”, and there are only five categories (four of the five categories are themselves infinite). The fifth category are the sporadic groups, which do not fit into any of the other categories. The first was discovered by Émile Mathieu in 1861, and between then and 1873 he found four more. As group theory continued to develop, mathematicians kept finding more and more of these sporadic groups, and nobody knew whether there were only a finite number or infinitely many of them…until recently.

Most research papers in mathematics are short and concise. Some group theory papers are the exception, with two hundred pagers packed with dense notation not uncommon. The classification theorem of finite groups is the ultimate outlier; it has been likened to the Manhattan Project of pure mathematics. Consisting of hundreds of papers published over decades by a large collection of authors, it is estimated, if every component involved in the proof were collected together, to be on the order of fifteen thousand pages, many of which are so technical those not involved in the work itself have extreme difficulty understanding them. (In fact, a “Revision project” is currently underway with the goal of restating the proof in a form which future generations of mathematicians will be able to comprehend.) The last part of the classification theorem, itself more than a thousand pages in length, was not put into place until November 2004, so only then could one say with complete confidence that there were only 26 sporadic groups, all of which are known.

While these groups are “simple” in the sense of not being able to be decomposed, the symmetries most of them represent are of mind-boggling complexity. The order of a finite group is the number of elements it contains; for example, the group of permutations on five items has an order of 5! = 120. The simplest sporadic group has an order of 7920 and the biggest, well, it's a monster. In fact, that's what it's called, the “monster group”, and its order is (deep breath):

808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 =
2⁴⁶×3²⁰×5⁹×7⁶×11²×13³×17×19×23×29×31×41×47×59×71 If it helps, you can think of the monster as the group of rotations in a space of 196,884 dimensions—much easier to visualise, isn't it? In any case, that's how Robert Griess first constructed the monster in 1982, in a 102 page paper done without a computer.

In one of those “take your breath away” connections between distant and apparently unrelated fields of mathematics, the divisors of the order of the monster are precisely the 15 supersingular primes, which are intimately related to the j-function of number theory. Other striking coincidences, or maybe deep connections, link the monster group to the Lorentzian geometry of general relativity, the multidimensional space of string theory, and the enigmatic properties of the number 163 in number theory. In 1983, Freeman Dyson mused, “I have a sneaking hope, a hope unsupported by any facts or any evidence, that sometime in the twenty-first century physicists will stumble upon the Monster group, built in some unsuspected way into the structure of the universe.” Hey, stranger things have happened.

This book, by a professional mathematician who is also a talented populariser of the subject, tells the story of this quest. During his career, he personally knew almost all of the people involved in the classification project, and leavens the technical details with biographical accounts and anecdotes of the protagonists. To avoid potentially confusing mathematical jargon, he uses his own nomenclature: “atom of symmetry” instead of finite simple group, “deconstruction” instead of decomposition, and so on. This sometimes creates its own confusion, since the extended quotes from mathematicians use the standard terminology; the reader should refer to the glossary at the end of the book to resolve any such puzzlement.

November 2006 

Seife, Charles. Zero: The Biography of a Dangerous Idea. New York: Penguin Books, 2000. ISBN 0-14-029647-6.

January 2002 

Stewart, Ian. Flatterland. Cambridge, MA: Perseus Publishing, 2001. ISBN 0-7382-0442-0.

May 2002 

Szpiro, George G. Kepler's Conjecture. Hoboken, NJ: John Wiley & Sons, 2003. ISBN 0-471-08601-0.

In 1611, Johannes Kepler conjectured that no denser arrangement of spheres existed than the way grocers stack oranges and artillerymen cannonballs. For more than 385 years this conjecture, something “many mathematicians believe, and all physicists know”, defied proof. Over the centuries, many distinguished mathematicians assaulted the problem to no avail. Then, in 1998, Thomas C. Hales, assisted by Samuel P. Ferguson, announced a massive computer proof of Kepler's conjecture in which, to date, no flaw has been found. Who would have imagined that a fundamental theorem in three-dimensional geometry would be proved by reducing it to a linear programming problem? This book sketches the history of Kepler's conjecture and those who have assaulted it over the centuries, and explains, in layman's language, the essentials of the proof. I found the organisation of the book less than ideal. The author works up to Kepler's general conjecture by treating the history of lattice packing and general packing in two dimensions, then the kissing and lattice packing problems in three dimensions, each in a separate chapter. Many of the same people occupied themselves with these problems over a long span of time, so there is quite a bit of duplication among these chapters and one has to make an effort not to lose track of the chronology, which keeps resetting at chapter boundaries. To avoid frightening general readers, the main text interleaves narrative and more technical sections set in a different type font and, in addition, most equations are relegated to appendices at the end of the book. There's also the irritating convention that numerical approximations are, for the most part, given to three or four significant digits without ellipses or any other indication they are not precise values. (The reader is warned of this in the preface, but it still stinks.) Finally, there are a number of factual errors in historical details. Quibbles aside, this is a worthwhile survey of the history and eventual conquest of one of the most easily stated, difficult to prove, and longest standing problems in mathematics. The proof of Kepler's conjecture and all the programs used in it are available on Thomas C. Hales' home page.

February 2004 

Taleb, Nassim Nicholas. The Black Swan. New York: Random House, 2007. ISBN 978-1-4000-6351-2.

If you are interested in financial markets, investing, the philosophy of science, modelling of socioeconomic systems, theories of history and historicism, or the rôle of randomness and contingency in the unfolding of events, this is a must-read book. The author largely avoids mathematics (except in the end notes) and makes his case in quirky and often acerbic prose (there's something about the French that really gets his goat) which works effectively.

The essential message of the book, explained by example in a wide variety of contexts is (and I'll be rather more mathematical here in the interest of concision) is that while many (but certainly not all) natural phenomena can be well modelled by a Gaussian (“bell curve”) distribution, phenomena in human society (for example, the distribution of wealth, population of cities, book sales by authors, casualties in wars, performance of stocks, profitability of companies, frequency of words in language, etc.) are best described by scale-invariant power law distributions. While Gaussian processes converge rapidly upon a mean and standard deviation and rare outliers have little impact upon these measures, in a power law distribution the outliers dominate.

Consider this example. Suppose you wish to determine the mean height of adult males in the United States. If you go out and pick 1000 men at random and measure their height, then compute the average, absent sampling bias (for example, picking them from among college basketball players), you'll obtain a figure which is very close to that you'd get if you included the entire male population of the country. If you replaced one of your sample of 1000 with the tallest man in the country, or with the shortest, his inclusion would have a negligible effect upon the average, as the difference from the mean of the other 999 would be divided by 1000 when computing the average. Now repeat the experiment, but try instead to compute mean net worth. Once again, pick 1000 men at random, compute the net worth of each, and average the numbers. Then, replace one of the 1000 by Bill Gates. Suddenly Bill Gates's net worth dwarfs that of the other 999 (unless one of them randomly happened to be Warren Buffett, say)—the one single outlier dominates the result of the entire sample.

Power laws are everywhere in the human experience (heck, I even found one in AOL search queries), and yet so-called “social scientists” (Thomas Sowell once observed that almost any word is devalued by preceding it with “social”) blithely assume that the Gaussian distribution can be used to model the variability of the things they measure, and that extrapolations from past experience are predictive of the future. The entry of many people trained in physics and mathematics into the field of financial analysis has swelled the ranks of those who naïvely assume human action behaves like inanimate physical systems.

The problem with a power law is that as long as you haven't yet seen the very rare yet stupendously significant outlier, it looks pretty much like a Gaussian, and so your model based upon that (false) assumption works pretty well—until it doesn't. The author calls these unimagined and unmodelled rare events “Black Swans”—you can see a hundred, a thousand, a million white swans and consider each as confirmation of your model that “all swans are white”, but it only takes a single black swan to falsify your model, regardless of how much data you've amassed and how long it has correctly predicted things before it utterly failed.

Moving from ornithology to finance, one of the most common causes of financial calamities in the last few decades has been the appearance of Black Swans, wrecking finely crafted systems built on the assumption of Gaussian behaviour and extrapolation from the past. Much of the current calamity in hedge funds and financial derivatives comes directly from strategies for “making pennies by risking dollars” which never took into account the possibility of the outlier which would wipe out the capital at risk (not to mention that of the lenders to these highly leveraged players who thought they'd quantified and thus tamed the dire risks they were taking).

The Black Swan need not be a destructive bird: for those who truly understand it, it can point the way to investment success. The original business concept of Autodesk was a bet on a Black Swan: I didn't have any confidence in our ability to predict which product would be a success in the early PC market, but I was pretty sure that if we fielded five products or so, one of them would be a hit on which we could concentrate after the market told us which was the winner. A venture capital fund does the same thing: because the upside of a success can be vastly larger than what you lose on a dud, you can win, and win big, while writing off 90% of all of the ventures you back. Investors can fashion a similar strategy using options and option-equivalent investments (for example, resource stocks with a high cost of production), diversifying a small part of their portfolio across a number of extremely high risk investments with unbounded upside while keeping the bulk in instruments (for example sovereign debt) as immune as possible to Black Swans.

There is much more to this book than the matters upon which I have chosen to expound here. What you need to do is lay your hands on this book, read it cover to cover, think it over for a while, then read it again—it is so well written and entertaining that this will be a joy, not a chore. I find it beyond charming that this book was published by Random House.

January 2009 

Taleb, Nassim Nicholas. Fooled by Randomness. 2nd. ed. New York: Random House, [2004] 2005. ISBN 978-0-8129-7521-5.

This book, which preceded the author's bestselling The Black Swan (January 2009), explores a more general topic: randomness and, in particular, how humans perceive and often misperceive its influence in their lives. As with all of Taleb's work, it is simultaneously quirky, immensely entertaining, and so rich in wisdom and insights that you can't possible absorb them all in a single reading.

The author's central thesis, illustrated from real-world examples, tests you perform on yourself, and scholarship in fields ranging from philosophy to neurobiology, is that the human brain evolved in an environment in which assessment of probabilities (and especially conditional probabilities) and nonlinear outcomes was unimportant to reproductive success, and consequently our brains adapted to make decisions according to a set of modular rules called “heuristics”, which researchers have begun to tease out by experimentation. While our brains are capable of abstract thinking and, with the investment of time required to master it, mathematical reasoning about probabilities, the parts of the brain we use to make many of the important decisions in our lives are the much older and more instinctual parts from which our emotions spring. This means that otherwise apparently rational people may do things which, if looked at dispassionately, appear completely insane and against their rational self-interest. This is particularly apparent in the world of finance, in which the author has spent much of his career, and which offers abundant examples of individual and collective delusional behaviour both before and after the publication of this work.

But let's step back from the arcane world of financial derivatives and consider a much simpler and easier to comprehend investment proposition: Russian roulette. A diabolical billionaire makes the following proposition: play a round of Russian roulette (put one cartridge in a six shot revolver, spin the cylinder to randomise its position, put the gun to your temple and pull the trigger). If the gun goes off, you don't receive any payoff and besides, you're dead. If there's just the click of the hammer falling on an empty chamber, you receive one million dollars. Further, as a winner, you're invited to play again on the same date next year, when the payout if you win will be increased by 25%, and so on in subsequent years as long as you wish to keep on playing. You can quit at any time and keep your winnings.

Now suppose a hundred people sign up for this proposition, begin to play the game year after year, and none chooses to take their winnings and walk away from the table. (For connoisseurs of Russian roulette, this is the variety of the game in which the cylinder is spun before each shot, not where the live round continues to advance each time the hammer drops on an empty chamber: in that case there would be no survivors beyond the sixth round.) For each round, on average, 1/6 of the players are killed and out of the game, reducing the number who play next year. Out of the original 100 players in the first round, one would expect, on average, around 83 survivors to participate in the second round, where the payoff will be 1.25 million.

What do we have, then, after ten years of this game? Again, on average, we expect around 16 survivors, each of whom will be paid more than seven million dollars for the tenth round alone, and who will have collected a total of more than 33 million dollars over the ten year period. If the game were to go on for twenty years, we would expect around 3 survivors from the original hundred, each of whom would have “earned” more than a third of a billion dollars each.

Would you expect these people to be regular guests on cable business channels, sought out by reporters from financial publications for their “hot hand insights on Russian roulette”, or lionised for their consistent and rapidly rising financial results? No—they would be immediately recognised as precisely what they were: lucky (and consequently very wealthy) fools who, each year they continue to play the game, run the same 1 in 6 risk of blowing their brains out.

Keep this Russian roulette analogy in mind the next time you see an interview with the “sizzling hot” hedge fund manager who has managed to obtain 25% annual return for his investors over the last five years, or when your broker pitches a mutual fund with a “great track record”, or you read the biography of a businessman or investor who always seems to have made the “right call” at the right time. All of these are circumstances in which randomness, and hence luck, plays an important part. Just as with Russian roulette, there will inevitably be big winners with a great “track record”, and they're the only ones you'll see because the losers have dropped out of the game (and even if they haven't yet they aren't newsworthy). So the question you have to ask yourself is not how great the track record of a given individual is, but rather the size of the original cohort from which the individual was selected at the start of the period of the track record. The rate hedge fund managers “blow up” and lose all of their investors' money in one disastrous market excursion is less than that of the players blown away in Russian roulette, but not all that much. There are a lot of trading strategies which will yield high and consistent returns until they don't, at which time they suffer sudden and disastrous losses which are always reported as “unexpected”. Unexpected by the geniuses who devised the strategy, the fools who put up the money to back it, and the clueless journalists who report the debacle, but entirely predictable to anybody who modelled the risks being run in the light of actual behaviour of markets, not some egghead's ideas of how they “should” behave.

Shall we try another? You go to your doctor for a routine physical, and as part of the laboratory work on your blood, she orders a screening test for a rare but serious disease which afflicts only one person in a thousand but which can be treated if detected early. The screening test has a 5% false positive rate (in 5% of the people tested who do not actually have the disease, it erroneously says that they do) and a 0% false negative rate (if you have the disease, the test will always report that you do). You return to the doctor's office for the follow-up visit and she tells you that you tested positive for the disease. What is the probability you actually have it?

Spoiler warning: Plot and/or ending details follow.   (Show Spoilers) (Hide Spoilers)

Did you answer 95%? If you did, you're among the large majority of people, not just among the general population but also practising clinicians, who come to the same conclusion. And you'd be just as wrong as them. In fact, the odds you have the disease are a little less than 2%. Here's how it works. Let's assume an ensemble of 10,000 randomly selected people are tested. On average, ten of these people will have the disease, and all of them will test positive for it (no false negatives). But among that population, 500 people who do not have the disease will also test positive due to the 5% false positive rate of the test. That means that, on average (it gets tedious repeating this, but the natterers will be all over me if I don't do so in every instance), there will be, of 10,000 people tested, a total of 510 positive results, of which 10 actually have the disease. Hence, if you're the recipient of a positive test result, the probability you have the disease is 10/510, or a tad less than 2%. So, before embarking upon a demanding and potentially dangerous treatment regime, you're well advised to get some other independent tests to confirm that you are actually afflicted.

Spoilers end here.   (Hide Spoilers)

In making important decisions in life, we often rely upon information from past performance and reputation without taking into account how much those results may be affected by randomness, luck, and the “survivor effect” (the Russian roulette players who brag of their success in the game are necessarily those who aren't yet dead). When choosing a dentist, you can be pretty sure that a practitioner who is recommended by a variety of his patients whom you respect will do an excellent job drilling your teeth. But this is not the case when choosing an oncologist, since all of the people who give him glowing endorsements are necessarily those who did not die under his care, even if their survival is due to spontaneous remission instead of the treatment they received. In such a situation, you need to, as it were, interview the dead alongside the survivors, or, that being difficult, compare the actual rate of survival among comparable patients with the same condition.

Even when we make decisions with our higher cognitive facilities rather than animal instincts, it's still easy to get it wrong. While the mathematics of probability and statistics have been put into a completely rigorous form, there are assumptions in how they are applied to real world situations which can lead to the kinds of calamities one reads about regularly in the financial press. One of the reasons physical scientists transmogrify so easily into Wall Street “quants” is that they are trained and entirely comfortable with statistical tools and probabilistic analysis. The reason they so frequently run off the cliff, taking their clients' fortunes in the trailer behind them, is that nature doesn't change the rules, nor does she cheat. Most physical processes will exhibit well behaved Gaussian or Poisson distributions, with outliers making a vanishingly small contribution to mean and median values. In financial markets and other human systems none of these conditions obtain: the rules change all the time, and often change profoundly before more than a few participants even perceive they have; any action in the market will provoke a reaction by other actors, often nonlinear and with unpredictable delays; and in human systems the Pareto and other wildly non-Gaussian power law distributions are often the norm.

We live in a world in which randomness reigns in many domains, and where we are bombarded with “news and information” which is probably in excess of 99% noise to 1% signal, with no obvious way to extract the signal except with the benefit of hindsight, which doesn't help in making decisions on what to do today. This book will dramatically deepen your appreciation of this dilemma in our everyday lives, and provide a philosophical foundation for accepting the rôle randomness and luck plays in the world, and how, looked at with the right kind of eyes (and investment strategy) randomness can be your friend.

February 2011 

Taleb, Nassim Nicholas. Antifragile. New York: Random House, 2012. ISBN 978-0-8129-7968-8.

This book is volume three in the author's Incerto series, following Fooled by Randomness (February 2011) and The Black Swan (January 2009). It continues to explore the themes of randomness, risk, and the design of systems: physical, economic, financial, and social, which perform well in the face of uncertainty and infrequent events with large consequences. He begins by posing the deceptively simple question, “What is the antonym of ‘fragile’?”

After thinking for a few moments, most people will answer with “robust” or one of its synonyms such as “sturdy”, “tough”, or “rugged”. But think about it a bit more: does a robust object or system actually behave in the opposite way to a fragile one? Consider a teacup made of fine china. It is fragile—if subjected to more than a very limited amount of force or acceleration, it will smash into bits. It is fragile because application of such an external stimulus, for example by dropping it on the floor, will dramatically degrade its value for the purposes for which it was created (you can't drink tea from a handful of sherds, and they don't look good sitting on the shelf). Now consider a teacup made of stainless steel. It is far more robust: you can drop it from ten kilometres onto a concrete slab and, while it may be slightly dented, it will still work fine and look OK, maybe even acquiring a little character from the adventure. But is this really the opposite of fragility? The china teacup was degraded by the impact, while the stainless steel one was not. But are there objects and systems which improve as a result of random events: uncertainty, risk, stressors, volatility, adventure, and the slings and arrows of existence in the real world? Such a system would not be robust, but would be genuinely “anti-fragile” (which I will subsequently write without the hyphen, as does the author): it welcomes these perturbations, and may even require them in order to function well or at all.

Antifragility seems an odd concept at first. Our experience is that unexpected events usually make things worse, and that the inexorable increase in entropy causes things to degrade with time: plants and animals age and eventually die; machines wear out and break; cultures and societies become decadent, corrupt, and eventually collapse. And yet if you look at nature, antifragility is everywhere—it is the mechanism which drives biological evolution, technological progress, the unreasonable effectiveness of free market systems in efficiently meeting the needs of their participants, and just about everything else that changes over time, from trends in art, literature, and music, to political systems, and human cultures. In fact, antifragility is a property of most natural, organic systems, while fragility (or at best, some degree of robustness) tends to characterise those which were designed from the top down by humans. And one of the paradoxical characteristics of antifragile systems is that they tend to be made up of fragile components.

How does this work? We'll get to physical systems and finance in a while, but let's start out with restaurants. Any reasonably large city in the developed world will have a wide variety of restaurants serving food from numerous cultures, at different price points, and with ambience catering to the preferences of their individual clientèles. The restaurant business is notoriously fragile: the culinary preferences of people are fickle and unpredictable, and restaurants who are behind the times frequently go under. And yet, among the population of restaurants in a given area at a given time, customers can usually find what they're looking for. The restaurant population or industry is antifragile, even though it is composed of fragile individual restaurants which come and go with the whims of diners, which will be catered to by one or more among the current, but ever-changing population of restaurants.

Now, suppose instead that some Food Commissar in the All-Union Ministry of Nutrition carefully studied the preferences of people and established a highly-optimised and uniform menu for the monopoly State Feeding Centres, then set up a central purchasing, processing, and distribution infrastructure to optimise the efficient delivery of these items to patrons. This system would be highly fragile, since while it would deliver food, there would no feedback based upon customer preferences, and no competition to respond to shifts in taste. The result would be a mediocre product which, over time, was less and less aligned with what people wanted, and hence would have a declining number of customers. The messy and chaotic market of independent restaurants, constantly popping into existence and disappearing like virtual particles, exploring the culinary state space almost at random, does, at any given moment, satisfy the needs of its customers, and it responds to unexpected changes by adapting to them: it is antifragile.

Now let's consider an example from metallurgy. If you pour molten metal from a furnace into a cold mould, its molecules, which were originally jostling around at random at the high temperature of the liquid metal, will rapidly freeze into a structure with small crystals randomly oriented. The solidified metal will contain dislocations wherever two crystals meet, with each forming a weak spot where the metal can potentially fracture under stress. The metal is hard, but brittle: if you try to bend it, it's likely to snap. It is fragile.

To render it more flexible, it can be subjected to the process of annealing, where it is heated to a high temperature (but below melting), which allows the molecules to migrate within the bulk of the material. Existing grains will tend to grow, align, and merge, resulting in a ductile, workable metal. But critically, once heated, the metal must be cooled on a schedule which provides sufficient randomness (molecular motion from heat) to allow the process of alignment to continue, but not to disrupt already-aligned crystals. Here is a video from Cellular Automata Laboratory which demonstrates annealing. Note how sustained randomness is necessary to keep the process from quickly “freezing up” into a disordered state.

In another document at this site, I discuss solving the travelling salesman problem through the technique of simulated annealing, which is analogous to annealing metal, and like it, is a manifestation of antifragility—it doesn't work without randomness.

When you observe a system which adapts and prospers in the face of unpredictable changes, it will almost always do so because it is antifragile. This is a large part of how nature works: evolution isn't able to predict the future and it doesn't even try. Instead, it performs a massively parallel, planetary-scale search, where organisms, species, and entire categories of life appear and disappear continuously, but with the ecosystem as a whole constantly adapting itself to whatever inputs may perturb it, be they a wholesale change in the composition of the atmosphere (the oxygen catastrophe at the beginning of the Proterozoic eon around 2.45 billion years ago), asteroid and comet impacts, and ice ages.

Most human-designed systems, whether machines, buildings, political institutions, or financial instruments, are the antithesis of those found in nature. They tend to be highly-optimised to accomplish their goals with the minimum resources, and to be sufficiently robust to cope with any stresses they may be expected to encounter over their design life. These systems are not antifragile: while they may be designed not to break in the face of unexpected events, they will, at best, survive, but not, like nature, often benefit from them.

The devil's in the details, and if you reread the last paragraph carefully, you may be able to see the horns and pointed tail peeking out from behind the phrase “be expected to”. The problem with the future is that it is full of all kinds of events, some of which are un-expected, and whose consequences cannot be calculated in advance and aren't known until they happen. Further, there's usually no way to estimate their probability. It doesn't even make any sense to talk about the probability of something you haven't imagined could happen. And yet such things happen all the time.

Today, we are plagued, in many parts of society, with “experts” the author dubs fragilistas. Often equipped with impeccable academic credentials and with powerful mathematical methods at their fingertips, afflicted by the “Soviet-Harvard delusion” (overestimating the scope of scientific knowledge and the applicability of their modelling tools to the real world), they are blind to the unknown and unpredictable, and they design and build systems which are highly fragile in the face of such events. A characteristic of fragilista-designed systems is that they produce small, visible, and apparently predictable benefits, while incurring invisible risks which may be catastrophic and occur at any time.

Let's consider an example from finance. Suppose you're a conservative investor interested in generating income from your lifetime's savings, while preserving capital to pass on to your children. You might choose to invest, say, in a diversified portfolio of stocks of long-established companies in stable industries which have paid dividends for 50 years or more, never skipping or reducing a dividend payment. Since you've split your investment across multiple companies, industry sectors, and geographical regions, your risk from an event affecting one of them is reduced. For years, this strategy produces a reliable and slowly growing income stream, while appreciation of the stock portfolio (albeit less than high flyers and growth stocks, which have greater risk and pay small dividends or none at all) keeps you ahead of inflation. You sleep well at night.

Then 2008 rolls around. You didn't do anything wrong. The companies in which you invested didn't do anything wrong. But the fragilistas had been quietly building enormous cross-coupled risk into the foundations of the financial system (while pocketing huge salaries and bonuses, while bearing none of the risk themselves), and when it all blows up, in one sickening swoon, you find the value of your portfolio has been cut by 50%. In a couple of months, you have lost half of what you worked for all of your life. Your “safe, conservative, and boring” stock portfolio happened to be correlated with all of the other assets, and when the foundation of the system started to crumble, suffered along with them. The black swan landed on your placid little pond.

What would an antifragile investment portfolio look like, and how would it behave in such circumstances? First, let's briefly consider a financial option. An option is a financial derivative contract which gives the purchaser the right, but not the obligation, to buy (“call option”) or sell (”put option”) an underlying security (stock, bond, market index, etc.) at a specified price, called the “strike price” (or just “strike”). If the a call option has a strike above, or a put option a strike below, the current price of the security, it is called “out of the money”, otherwise it is “in the money”. The option has an expiration date, after which, if not “exercised” (the buyer asserts his right to buy or sell), the contract expires and the option becomes worthless.

Let's consider a simple case. Suppose Consolidated Engine Sludge (SLUJ) is trading for US$10 per share on June 1, and I buy a call option to buy 100 shares at US$15/share at any time until August 31. For this right, I might pay a premium of, say, US$7. (The premium depends upon sellers' perception of the volatility of the stock, the term of the option, and the difference between the current price and the strike price.) Now, suppose that sometime in August, SLUJ announces a breakthrough that allows them to convert engine sludge into fructose sweetener, and their stock price soars on the news to US$19/share. I might then decide to sell on the news, exercise the option, paying US$1500 for the 100 shares, and then immediately sell them at US$19, realising a profit of US$400 on the shares or, subtracting the cost of the option, US$393 on the trade. Since my original investment was just US$7, this represents a return of 5614% on the original investment, or 22457% annualised. If SLUJ never touches US$15/share, come August 31, the option will expire unexercised, and I'm out the seven bucks. (Since options can be bought and sold at any time and prices are set by the market, it's actually a bit more complicated than that, but this will do for understanding what follows.)

You might ask yourself what would motivate somebody to sell such an option. In many cases, it's an attractive proposition. If I'm a long-term shareholder of SLUJ and have found it to be a solid but non-volatile stock that pays a reasonable dividend of, say, two cents per share every quarter, by selling the call option with a strike of 15, I pocket an immediate premium of seven cents per share, increasing my income from owning the stock by a factor of 4.5. For this, I give up the right to any appreciation should the stock rise above 15, but that seems to be a worthwhile trade-off for a stock as boring as SLUJ (at least prior to the news flash).

A put option is the mirror image: if I bought a put on SLUJ with a strike of 5, I'll only make money if the stock falls below 5 before the option expires.

Now we're ready to construct a genuinely antifragile investment. Suppose I simultaneously buy out of the money put and call options on the same security, a so-called “long straddle”. Now, as long as the price remains within the strike prices of the put and call, both options will expire worthless, but if the price either rises above the call strike or falls below the put strike, that option will be in the money and pay off the further the underlying price veers from the band defined by the two strikes. This is, then, a pure bet on volatility: it loses a small amount of money as long as nothing unexpected happens, but when a shock occurs, it pays off handsomely.

Now, the premiums on deep out of the money options are usually very modest, so an investor with a portfolio like the one I described who was clobbered in 2008 could have, for a small sum every quarter, purchased put and call options on, say, the Standard & Poor's 500 stock index, expecting to usually have them expire worthless, but under the circumstance which halved the value of his portfolio, would pay off enough to compensate for the shock. (If worried only about a plunge he could, of course, have bought just the put option and saved money on premiums, but here I'm describing a pure example of antifragility being used to cancel fragility.)

I have only described a small fraction of the many topics covered in this masterpiece, and described none of the mathematical foundations it presents (which can be skipped by readers intimidated by equations and graphs). Fragility and antifragility is one of those concepts, simple once understood, which profoundly change the way you look at a multitude of things in the world. When a politician, economist, business leader, cultural critic, or any other supposed thinker or expert advocates a policy, you'll learn to ask yourself, “Does this increase fragility?” and have the tools to answer the question. Further, it provides an intellectual framework to support many of the ideas and policies which libertarians and advocates of individual liberty and free markets instinctively endorse, founded in the way natural systems work. It is particularly useful in demolishing “green” schemes which aim at replacing the organic, distributed, adaptive, and antifragile mechanisms of the market with coercive, top-down, and highly fragile central planning which cannot possibly have sufficient information to work even in the absence of unknowns in the future.

There is much to digest here, and the ramifications of some of the clearly-stated principles take some time to work out and fully appreciate. Indeed, I spent more than five years reading this book, a little bit at a time. It's worth taking the time and making the effort to let the message sink in and figure out how what you've learned applies to your own life and act accordingly. As Fat Tony says, “Suckers try to win arguments; nonsuckers try to win.”

April 2018 

Taleb, Nassim Nicholas. Skin in the Game. New York: Random House, 2018. ISBN 978-0-425-28462-9.

This book is volume four in the author's Incerto series, following Fooled by Randomness (February 2011), The Black Swan (January 2009), and Antifragile (April 2018). In it, he continues to explore the topics of uncertainty, risk, decision making under such circumstances, and how both individuals and societies winnow out what works from what doesn't in order to choose wisely among the myriad alternatives available.

The title, “Skin in the Game”, is an aphorism which refers to an individual's sharing the risks and rewards of an undertaking in which they are involved. This is often applied to business and finance, but it is, as the author demonstrates, a very general and powerful concept. An airline pilot has skin in the game along with the passengers. If the plane crashes and kills everybody on board, the pilot will die along with them. This insures that the pilot shares the passengers' desire for a safe, uneventful trip and inspires confidence among them. A government “expert” putting together a “food pyramid” to be vigorously promoted among the citizenry and enforced upon captive populations such as school children or members of the armed forces, has no skin in the game. If his or her recommendations create an epidemic of obesity, type 2 diabetes, and cardiovascular disease, that probably won't happen until after the “expert” has retired and, in any case, civil servants are not fired or demoted based upon the consequences of their recommendations.

Ancestral human society was all about skin in the game. In a small band of hunter/gatherers, everybody can see and is aware of the actions of everybody else. Slackers who do not contribute to the food supply are likely to be cut loose to fend for themselves. When the hunt fails, nobody eats until the next kill. If a conflict develops with a neighbouring band, those who decide to fight instead of running away or surrendering are in the front line of the battle and will be the first to suffer in case of defeat.

Nowadays we are far more “advanced”. As the author notes, “Bureaucracy is a construction by which a person is conveniently separated from the consequences of his or her actions.” As populations have exploded, layers and layers of complexity have been erected, removing authority ever farther from those under its power. We have built mechanisms which have immunised a ruling class of decision makers from the consequences of their decisions: they have little or no skin in the game.

Less than a third of all Roman emperors died in their beds. Even though they were at the pinnacle of the largest and most complicated empire in the West, they regularly paid the ultimate price for their errors either in battle or through palace intrigue by those dissatisfied with their performance. Today the geniuses responsible for the 2008 financial crisis, which destroyed the savings of hundreds of millions of innocent people and picked the pockets of blameless taxpayers to bail out the institutions they wrecked, not only suffered no punishment of any kind, but in many cases walked away with large bonuses or golden parachute payments and today are listened to when they pontificate on the current scene, rather than being laughed at or scorned as they would be in a rational world. We have developed institutions which shift the consequences of bad decisions from those who make them to others, breaking the vital feedback loop by which we converge upon solutions which, if not perfect, at least work well enough to get the job done without the repeated catastrophes that result from ivory tower theories being implemented on a grand scale in the real world.

Learning and Evolution

Being creatures who have evolved large brains, we're inclined to think that learning is something that individuals do, by observing the world, drawing inferences, testing hypotheses, and taking on knowledge accumulated by others. But the overwhelming majority of creatures who have ever lived, and of those alive today, do not have large brains—indeed, many do not have brains at all. How have they learned to survive and proliferate, filling every niche on the planet where environmental conditions are compatible with biochemistry based upon carbon atoms and water? How have they, over the billions of years since life arose on Earth, inexorably increased in complexity, most recently producing a species with a big brain able to ponder such questions?

The answer is massive parallelism, exhaustive search, selection for survivors, and skin in the game, or, putting it all together, evolution. Every living creature has skin in the ultimate game of whether it will produce offspring that inherit its characteristics. Every individual is different, and the process of reproduction introduces small variations in progeny. Change the environment, and the characteristics of those best adapted to reproduce in it will shift and, eventually, the population will consist of organisms adapted to the new circumstances. The critical thing to note is that while each organism has skin in the game, many may, and indeed must, lose the game and die before reproducing. The individual organism does not learn, but the species does and, stepping back another level, the ecosystem as a whole learns and adapts as species appear, compete, die out, or succeed and proliferate. This simple process has produced all of the complexity we observe in the natural world, and it works because every organism and species has skin in the game: its adaptation to its environment has immediate consequences for its survival.

None of this is controversial or new. What the author has done in this book is to apply this evolutionary epistemology to domains far beyond its origins in biology—in fact, to almost everything in the human experience—and demonstrate that both success and wisdom are generated when this process is allowed to work, but failure and folly result when it is thwarted by institutions which take the skin out of the game.

How does this apply in present-day human society? Consider one small example of a free market in action. The restaurant business is notoriously risky. Restaurants come and go all the time, and most innovations in the business fall flat on their face and quickly disappear. And yet most cities have, at any given time, a broad selection of restaurants with a wide variety of menus, price points, ambiance, and service to appeal to almost any taste. Each restaurant has skin in the game: those which do not attract sufficient customers (or, having once been successful, fail to adapt when customers' tastes change) go out of business and are replaced by new entrants. And yet for all the churning and risk to individual restaurants, the restaurant “ecosystem” is remarkably stable, providing customers options closely aligned with their current desires.

To a certain kind of “expert” endowed with a big brain (often crammed into a pointy head), found in abundance around élite universities and government agencies, all of this seems messy, chaotic, and (the horror!) inefficient. Consider the money lost when a restaurant fails, the cooks and waiters who lose their jobs, having to find a new restaurant to employ them, the vacant building earning nothing for its owner until a new tenant is found—certainly there must be a better way. Why, suppose instead we design a standardised set of restaurants based upon a careful study of public preferences, then roll out this highly-optimised solution to the problem. They might be called “public feeding centres”. And they would work about as well as the name implies.

Survival and Extinction

Evolution ultimately works through extinction. Individuals who are poorly adapted to their environment (or, in a free market, companies which poorly serve their customers) fail to reproduce (or, in the case of a company, survive and expand). This leaves a population better adapted to its environment. When the environment changes, or a new innovation appears (for example, electricity in an age dominated by steam power), a new sorting out occurs which may see the disappearance of long-established companies that failed to adapt to the new circumstances. It is a tautology that the current population consists entirely of survivors, but there is a deep truth within this observation which is at the heart of evolution. As long as there is a direct link between performance in the real world and survival—skin in the game—evolution will work to continually optimise and refine the population as circumstances change.

This evolutionary process works just as powerfully in the realm of ideas as in biology and commerce. Ideas have consequences, and for the process of selection to function, those consequences, good or ill, must be borne by those who promulgate the idea. Consider inventions: an inventor who creates something genuinely useful and brings it to market (recognising that there are many possible missteps and opportunities for bad luck or timing to disrupt this process) may reap great rewards which, in turn, will fund elaboration of the original invention and development of related innovations. The new invention may displace existing technologies and cause them, and those who produce them, to become obsolete and disappear (or be relegated to a minor position in the market). Both the winner and loser in this process have skin in the game, and the outcome of the game is decided by the evaluation of the customers expressed in the most tangible way possible: what they choose to buy.

Now consider an academic theorist who comes up with some intellectual “innovation” such as “Modern Monetary Theory” (which basically says that a government can print as much paper money as it wishes to pay for what it wants without collecting taxes or issuing debt as long as full employment has not been achieved). The theory and the reputation of those who advocate it are evaluated by their peers: other academics and theorists employed by institutions such as national treasuries and central banks. Such a theory is not launched into a market to fend for itself among competing theories: it is “sold” to those in positions of authority and imposed from the top down upon an economy, regardless of the opinions of those participating in it. Now, suppose the brilliant new idea is implemented and results in, say, total collapse of the economy and civil society? What price do those who promulgated the theory and implemented it pay? Little or nothing, compared to the misery of those who lost their savings, jobs, houses, and assets in the calamity. Many of the academics will have tenure and suffer no consequences whatsoever: they will refine the theory, or else publish erudite analyses of how the implementation was flawed and argue that the theory “has never been tried”. Some senior officials may be replaced, but will doubtless land on their feet and continue to pull down large salaries as lobbyists, consultants, or pundits. The bureaucrats who patiently implemented the disastrous policies are civil servants: their jobs and pensions are as eternal as anything in this mortal sphere. And, before long, another bright, new idea will bubble forth from the groves of academe.

(If you think this hypothetical example is unrealistic, see the career of one Robert Rubin. “Bob”, during his association with Citigroup between 1999 and 2009, received total compensation of US$126 million for his “services” as a director, advisor, and temporary chairman of the bank, during which time he advocated the policies which eventually brought it to the brink of collapse in 2008 and vigorously fought attempts to regulate the financial derivatives which eventually triggered the global catastrophe. During his tenure at Citigroup, shareholders of its stock lost 70% of their investment, and eventually the bank was bailed out by the federal government using money taken by coercive taxation from cab drivers and hairdressers who had no culpability in creating the problems. Rubin walked away with his “winnings” and paid no price, financial, civil, or criminal, for his actions. He is one of the many poster boys and girls for the “no skin in the game club”. And lest you think that, chastened, the academics and pointy-heads in government would regain their grounding in reality, I have just one phrase for you, “trillion dollar coin”, which “Nobel Prize” winner Paul Krugman declared to be “the most important fiscal policy debate of our lifetimes”.)

Intellectual Yet Idiot

A cornerstone of civilised society, dating from at least the Code of Hammurabi (c. 1754 B.C.), is that those who create risks must bear those risks: an architect whose building collapses and kills its owner is put to death. This is the fundamental feedback loop which enables learning. When it is broken, when those who create risks (academics, government policy makers, managers of large corporations, etc.) are able to transfer those risks to others (taxpayers, those subject to laws and regulations, customers, or the public at large), the system does not learn; evolution breaks down; and folly runs rampant. This phenomenon is manifested most obviously in the modern proliferation of the affliction the author calls the “intellectual yet idiot” (IYI). These are people who are evaluated by their peers (other IYIs), not tested against the real world. They are the equivalent of a list of movies chosen based upon the opinions of high-falutin' snobbish critics as opposed to box office receipts. They strive for the approval of others like themselves and, inevitably, spiral into ever more abstract theories disconnected from ground truth, ascending ever higher into the sky.

Many IYIs achieve distinction in one narrow field and then assume that qualifies them to pronounce authoritatively on any topic whatsoever. As was said by biographer Roy Harrod of John Maynard Keynes,

He held forth on a great range of topics, on some of which he was thoroughly expert, but on others of which he may have derived his views from the few pages of a book at which he happened to glance. The air of authority was the same in both cases.

Still other IYIs have no authentic credentials whatsoever, but derive their purported authority from the approbation of other IYIs in completely bogus fields such as gender and ethnic studies, critical anything studies, and nutrition science. As the author notes, riding some of his favourite hobby horses,

Typically, the IYI get first-order logic right, but not second-order (or higher) effects, making him totally incompetent in complex domains.

The IYI has been wrong, historically, about Stalinism, Maoism, Iraq, Libya, Syria, lobotomies, urban planning, low-carbohydrate diets, gym machines, behaviorism, trans-fats, Freudianism, portfolio theory, linear regression, HFCS (High-Fructose Corn Syrup), Gaussianism, Salafism, dynamic stochastic equilibrium modeling, housing projects, marathon running, selfish genes, election-forecasting models, Bernie Madoff (pre-blowup), and p values. But he is still convinced his current position is right.

Doubtless, IYIs have always been with us (at least since societies developed to such a degree that they could afford some fraction of the population who devoted themselves entirely to words and ideas)—Nietzsche called them “Bildungsphilisters”—but since the middle of the twentieth century they have been proliferating like pond scum, and now hold much of the high ground in universities, the media, think tanks, and senior positions in the administrative state. They believe their models (almost always linear and first-order) accurately describe the behaviour of complex dynamic systems, and that they can “nudge” the less-intellectually-exalted and credentialed masses into virtuous behaviour, as defined by them. When the masses dare to push back, having a limited tolerance for fatuous nonsense, or being scolded by those who have been consistently wrong about, well, everything, and dare vote for candidates and causes which make sense to them and seem better-aligned with the reality they see on the ground, they are accused of—gasp—populism, and must be guided in the proper direction by their betters, their uncouth speech silenced in favour of the cultured “consensus” of the few.

One of the reasons we seem to have many more IYIs around than we used to, and that they have more influence over our lives is related to scaling. As the author notes, “it is easier to macrobull***t than microbull***t”. A grand theory which purports to explain the behaviour of billions of people in a global economy over a period of decades is impossible to test or verify analytically or by simulation. An equally silly theory that describes things within people's direct experience is likely to be immediately rejected out of hand as the absurdity it is. This is one reason decentralisation works so well: when you push decision making down as close as possible to individuals, their common sense asserts itself and immunises them from the blandishments of IYIs.

The Lindy Effect

How can you sift the good and the enduring from the mass of ephemeral fads and bad ideas that swirl around us every day? The Lindy effect is a powerful tool. Lindy's delicatessen in New York City was a favoured hangout for actors who observed that the amount of time a show had been running on Broadway was the best predictor of how long it would continue to run. A show that has run for three months will probably last for at least three months more. A show that has made it to the one year mark probably has another year or more to go. In other words, the best test for whether something will stand the test of time is whether it has already withstood the test of time. This may, at first, seem counterintuitive: a sixty year old person has a shorter expected lifespan remaining than a twenty year old. The Lindy effect applies only to nonperishable things such as “ideas, books, technologies, procedures, institutions, and political systems”.

Thus, a book which has been in print continuously for a hundred years is likely to be in print a hundred years from now, while this season's hot best-seller may be forgotten a few years hence. The latest political or economic theory filling up pages in the academic journals and coming onto the radar of the IYIs in the think tanks, media punditry, and (shudder) government agencies, is likely to be forgotten and/or discredited in a few years while those with a pedigree of centuries or millennia continue to work for those more interested in results than trendiness.

Religion is Lindy. If you disregard all of the spiritual components to religion, long-established religions are powerful mechanisms to transmit accumulated wisdom, gained through trial-and-error experimentation and experience over many generations, in a ready-to-use package for people today. One disregards or scorns this distilled experience at one's own great risk. Conversely, one should be as sceptical about “innovation” in ancient religious traditions and brand-new religions as one is of shiny new ideas in any other field.

(A few more technical notes…. As I keep saying, “Once Pareto gets into your head, you'll never get him out.” It's no surprise to find that the Lindy effect is deeply related to the power-law distribution of many things in human experience. It's simply another way to say that the lifetime of nonperishable goods is distributed according to a power law just like incomes, sales of books, music, and movie tickets, use of health care services, and commission of crimes. Further, the Lindy effect is similar to J. Richard Gott's Copernican statement of the Doomsday argument, with the difference that Gott provides lower and upper bounds on survival time for a given confidence level predicted solely from a random observation that something has existed for a known time.)

Uncertainty, Risk, and Decision Making

All of these observations inform dealing with risk and making decisions based upon uncertain information. The key insight is that in order to succeed, you must first survive. This may seem so obvious as to not be worth stating, but many investors, including those responsible for blow-ups which make the headlines and take many others down with them, forget this simple maxim. It is deceptively easy to craft an investment strategy which will yield modest, reliable returns year in and year out—until it doesn't. Such strategies tend to be vulnerable to “tail risks”, in which an infrequently-occurring event (such as 2008) can bring down the whole house of cards and wipe out the investor and the fund. Once you're wiped out, you're out of the game: you're like the loser in a Russian roulette tournament who, after the gun goes off, has no further worries about the probability of that event. Once you accept that you will never have complete information about a situation, you can begin to build a strategy which will prevent your blowing up under any set of circumstances, and may even be able to profit from volatility. This is discussed in more detail in the author's earlier Antifragile.

The Silver Rule

People and institutions who have skin in the game are likely to act according to the Silver Rule: “Do not do to others what you would not like them to do to you.” This rule, combined with putting the skin of those “defence intellectuals” sitting in air-conditioned offices into the games they launch in far-off lands around the world, would do much to save the lives and suffering of the young men and women they send to do their bidding.

August 2019 

Wells, David. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin Books, 1991. ISBN 0-14-011813-6.

What a treat—two hundred and seventy-five diagram-rich pages covering hundreds of geometrical curiosities ranging from the problem of Apollonius to zonohedra. Items range from classical Euclidean geometry to modern topics such as higher dimensional space, non-Euclidean geometry, and topological transformations; and from classical times until the present—it's amazing how many fundamental properties of objects as simple as triangles were discovered only in the twentieth century!

There are so many wonders here I shall not attempt to list them but simply commend this book to your own exploration and enjoyment. But one example…it's obvious that a non-convex room with black walls cannot be illuminated by a single light placed within it. But what if all the walls are mirrors? It is possible to design a mirrored room such that a light within it will still leave some part dark (p. 263)? The illustration of the Voderberg tile on p. 268 is unfortunate; the width of the lines makes it appear not to be a proper tile, but rather two tiles joined at a point. This page shows a detailed construction which makes it clear that the tile is indeed well formed and rigid.

I will confess, as a number nerd more than a geometry geek, that this book comes in second in my estimation behind the author's Penguin Book of Curious and Interesting Numbers, one single entry of which motivated me to consume three years of computer time in 1987–1990. But there are any number of wonders here, and the individual items are so short you can open the book at random and find something worth reading you can finish in a minute or so. Almost all items are given without proof, but there are citations to publications for many and you'll be able to find most of the rest on MathWorld.

March 2007 

Wilson, Robin. Four Colors Suffice. Princeton: Princeton University Press, 2002. ISBN 0-691-11533-8.

October 2003 

Wolfram, Stephen. A New Kind of Science. Champaign, IL: Wolfram Media, 2002. ISBN 1-57955-008-8.

The full text of this book may now be read online.

August 2002