Copyright 1985, Journal of Parapsychology. Reproduced with permission. To purchase a complete issue write Journal of Parapsychology, 402 N. Buchanan Blvd., Durham, NC 27701, USA (journal@rhine.org). For copies of complete articles, write The Genuine Article, ISI, 3501 Market St., Philadelphia, PA 19104, USA.

ADDITION EFFECT FOR PK ON PRERECORDED TARGETS

BY HELMUT SCHMIDT

Originally published in Journal of Parapsychology, Vol. 49, Sept. 1985

ABSTRACT: In the reported experiments, prerecorded binary events were exposed to two consecutive PK efforts, sometimes in the same target direction and sometimes in opposite target directions. The question under study was whether the two PK efforts would contribute equally to the outcome (which is the null hypothesis) or whether the first effort would have a stronger effect. The results reject the null hypothesis (p = .02) and suggest that the observation of the prerecorded events by the first subject may lock in these events so that any subsequent PK attempt can have no effect.

One of the most interesting questions raised by previous PK experiments with prerecorded targets is what happens if two consecutive PK efforts are made on the same targets. Do the two efforts add linearly or does the first effort have the greater weight?

When PK effects with prerecorded targets were first reported (Schmidt, 1976), two different interpretations of the effects were offered. One was based on a "teleological" psi model in which the time order between cause and effect was taken to be inverted, so that a later PK effort by a subject might affect the outcome of an earlier random event. The other interpretation, based on a "quantum collapse" model, borrowed ideas from quantum theory and suggested that nature makes the final decision on the outcome of a random event only at the time when the outcome is noticed by some human observer. In other words, the PK mechanism on prerecorded targets would not have to act on the past. Rather, the PK subject, as the first observer of the result, would make nature decide between two still possible outcomes.

These different interpretations and the associated psi models have recently been discussed in detail (Schmidt, 1984). For the experiments reported here, the two models make very different predictions. The teleological model implies (for relatively weak effects) a linear addition of subsequent PK efforts. And, in particular, it implies that the time sequence of two different PK efforts should be of no importance for the result. In the quantum collapse model, however, the first of the two PK efforts should have the main effect: after the first subject makes the PK effort and observes all (or most) of the results, nature would be forced to decide the real outcome, and nothing (or little) would be left to change as a result of a subsequent PK effort.

To have a specific and manageable objective, I conducted a set of three experiments that would test the following statement of the teleological model. This is the "null hypothesis":

If two PK efforts, A and B, are made on the same prerecorded random events, and if the subjects are blind to the test conditions, then the scores are independent of whether the effort A or B was made first.

At the start of each of the three experiments, a sufficiently long string of binary events was generated with the help of radioactive decays as the source of randomness. These events were stored on permanent memory chips as sequences of 1's and 0's. For a test run, a section of the prerecorded events was displayed sequentially while the subjects tried to enforce a high number of target events. Either the 1's or the 0's could be displayed as "hits" without the subjects' being aware of the difference. In this arrangement, it was easy to present the same binary sequence to two subjects and to direct the two PK efforts either in the same target direction or in opposite target directions.

The first experiment was slightly different insofar as the two consecutive PK efforts were made by the same subject, whereas in the other two experiments, there were two subjects, a pretested PK subject and a control subject who had no established PK ability. Another minor difference was in the display. The first experiment used auditory feedback in the form of different clicks for the hits and misses, whereas the other experiments used a visual display.

TWO PK EFFORTS BY ONE SUBJECT

(EXPERIMENT 1)

In the first experiment, I as subject made consecutive PK efforts on the same prerecorded random events. In half the trials, the two efforts were aimed in the same direction, but in the other half one effort was aimed at obtaining many 1's and the other at obtaining many 0's. This latter situation was particularly relevant to the null hypothesis. If the time sequence of two efforts does not matter, then two efforts in opposite directions would cancel each other, whereas in the competing model, the first effort would override the second one.

Prerecording the Random Events

As the first step, a sequence of 5,120 random bits (a random sequence of 0's and 1's) was recorded on a memory chip.

To generate the random numbers, I used a small, inexpensive computer (Micro-Professor MPF-1 from Multitech Electronics, Inc.) with a Geiger counter attachment (Schmidt, 1977). The same computer was also used in the test sessions to display the recorded sequences.

The simplicity of the computer made the random number generation particularly clean (more sophisticated computers have built-in interrupt procedures that may interfere). But as a double safeguard against malfunctions, I used random number tables to "reshuffle" the initially generated random numbers as follows:

I subdivided the initial 5,120-bit sequence into 160 consecutive sections of 32 bits. I then used a binary 160-bit sequence derived from a random number table to invert (interchange 1 and 0 in the section) about half the sections randomly. To save the obtained final random numbers, I recorded them on a permanent memory chip (EPROM 2532).

There was one last possibility of malfunction to guard against: During the shuffling process or the subsequent recording, something might go wrong. Therefore, I also saved the initial sequence of random numbers on a permanent memory chip. Then at the end of the experiment, I repeated the reshuffling procedure on the initial numbers sequence and verified the accuracy of the final sequence used in the experiment.

The Computer in a Test Session

The 5,120 random bits for the test runs filled only a small part of the memory chip. The rest of the memory held the computer program (written in machine language for the Z80 microprocessor) and a sufficient supply of random bits for "play runs," which were for practice and warm-up before the test runs. With the chip inserted into the computer, the experiment could begin.

To start a test run or a play run, the subject entered a 4-digit code number, which specified the 128-bit section of prerecorded random numbers to be used for the run. And at the push of a button, the test run started.

The auditory display was clicks. They were administered either simultaneously to both headphones and thereby perceived at the center of the head, or alternatively between the right and the left headphone and thereby perceived at the sides of the head. Depending on the test conditions, a 1 in the bit sequence was accompanied by a pair of center clicks and a 0 by a pair of side clicks, or vice versa.

In programming the feedback, I used the following symbols: R for a click in right ear; L, a click in the left ear; C, a center click (R and L); P, a pause between clicks. The patterns for the two types of feedback signal were written:

Center clicks: C P P C P P
Side clicks: R P L P R P L P.

(I needed double pauses between the center clicks to make their frequency appear equal to the frequency of a sequence of side clicks.)

The duration of a run of 128 bits was approximately 15 sec. With nearly negligible duration of the clicks, this gave a value of about 1/30 sec for the duration of the pauses.

For each run, two decisions had to be made in advance: The first was whether the subject's PK effort should be for many 0's or many 1's (designation of 0's or 1's as hits). The second was whether he wanted to aim either at (a high number of) center clicks or at side clicks. The proper correspondence between center and side clicks on the one hand and 0's and 1's on the other were made under the control of two switches to be set at the start of a run.

The experiment was designed so that for half of the prerecorded bits the PK efforts were made in the same direction, whereas on the other half the two efforts were opposite (one effort toward a 1 and one effort toward a 0). For reasons discussed below, it seemed desirable to interweave these two situations within each run. Therefore, an assignment switch was provided with the following function:

With the switch in the UP position, each 1 was displayed as a hit. With the switch in the DOWN position, the even-numbered bits were still displayed as hits if they contained a 1. The odd-numbered bits, however, were now displayed as a hit if they contained a 0.

During the experiment each run was displayed once with the switch in the UP position and once in the DOWN position. Then, the two PK efforts on the even-numbered bits were both aimed at obtaining a 1, but the odd-numbered bits were subject to PK efforts in opposite directions.

A second switch, the target-selection switch, allowed the subject to have the hits (specified by setting the assignment switch) displayed as either center clicks or side clicks. In this manner, the subject could always choose the goal he happened to prefer at the moment.

Keeping the Subject Ignorant of the Conditions

In this experiment, the focus was on the basic psi mechanism rather than on psychological factors. Therefore, it was necessary to offer the physically different test conditions in psychologically identical settings. In particular, I, the subject, should not know whether my effort was the first or second attempt at the targets or whether the two efforts were aimed in the same or in opposite directions. Some special precautions were required because I acted simultaneously in the role of experimenter and subject.

At the start of each test run, I entered, from a prepared list, a coded run number and the setting of the assignment switch (UP or DOWN). The run number determined which section of the prerecorded binary bits would be used, and the switch setting specified the assignment of 1's or 0's as PK targets. The run number had to be provided in encoded form (see below) because I should not recognize when a previously presented binary sequence was used for the second time.

The possibility that I might remember the click pattern and in this manner recognize the run at the second presentation was excluded by the above-mentioned method of partial inversion (of the odd-numbered bits) at the second presentation of the binary sequence.

Appendix A describes some details of how the run numbers were encoded and how a proper sequence of run assignments was prepared.

Test Sessions and Results

During a typical run of 15 sec's duration, I listened through headphones to the two types of clicks, one type appearing in the center of the head and the other closer to the sides of the head. Some subjects find this display very attractive because the PK effort has to be directed, not toward some external machine, but toward signals felt very close by, inside the head.

If one were to try classifying the many possible forms of PK feedback, one parameter for ranking the displays would be the correlation between the actual run score and the subject's estimate of the score (before the score was displayed numerically). With the pendulum display used in the two later experiments, for example, the subject knew fairly well at the end of the run whether the total result was good or bad. The present two-click display, however, seems to be on the other end of the scale. Even though the subject can follow the display of the individual hits and misses, the mind does not seem to integrate the scores easily, and the subject only rarely feels certain about the positive or negative outcome of a run.

Related to this feature of the two-click display may be the somewhat surprising pattern that I myself noticed: In many practice runs, always aimed at center clicks, there was no indication of consistent hitting. Instead, strings of unusually high scoring were mixed with strings of unusually high missing. It was as if the mind's attention had uncontrollably flipped from one task to the other. It might be very interesting to try to confirm this effect in work with a variety of subjects.

For the present study, I only wanted reliably high scores so that I could study the addition effect. Therefore, I began each test session with a large number (up to 50) of practice runs, waiting until the scores indicated a positive pattern. Only then did I start a sequence of test runs.

A test run was initiated by entering the next encoded run number and setting the assignment switch. The setting of a further switch specified my goal, which was mostly a high number of center clicks rather than side clicks. For a practice run, the run number 0000 had to be entered. There, the timing of the corresponding button pushes provided enough randomness for the starting point of a 128-bit sequence in a special random number block (containing over 16,000 bits) of the memory chip. At the end of each run, the computer displayed the number of hits (expectation value = 64).

Ten test sessions were held over a 3-week period in February 1984. All test sessions were preceded by practice runs. In about half of the attempts, these practice runs did not lead to encouraging scoring. In those cases no test sessions were held on that day.

For analysis of the results, each run score (deviation of the number of hits from chance) is subdivided into two contributions: (a) the score S(even) obtained on the even-numbered binary events on which the subject made two consecutive PK efforts in the same direction; and (b) the score S(odd) on the odd-numbered bits where two efforts in opposite directions were made. In the latter case, let us define a score as positive if the deviation is in the direction of the first PK effort.

Each of these two conditions comprises 2,560 binary events. The obtained deviations with their corresponding Z values are:

S(even) = 46, Z(even) = 1.82

S(odd) = 18, Z(odd) = 0.71 = Z(1).

Preliminary Discussion

Since this is only the first of three experiments performed to test a specific hypothesis, the final analysis will be given later.

Permit me at this stage to make some casual remarks on the results:

1. S(even) suggests (p = .03) that there was a PK effect where I definitely expected it, that is, when the two efforts occurred in the same direction.

2. Under the null hypothesis, S(odd) should average to zero, whereas the counterhypothesis would predict a positive value. The obtained Z value, Z(1) = 0.71, in itself, is not large enough to provide strong support for the counterhypothesis. There, we have to wait until we have the corresponding Z values - Z(2) and Z(3) - from the other two experiments.

For the test of the null hypothesis, only the results of the odd trials are interesting, and the reader may wonder why the even-numbered trials, with two efforts in the same direction, were included in the experiment at all. The reason was that I wanted to give the subject a fair chance to succeed, no matter whether the null hypothesis was correct. With the null hypothesis correct, the odd-numbered trials alone would give chance scoring, independent of the subject's efforts and PK abilities.

In this experiment, the binary events were presented at high speed, about 8 events per second, so that the subject might not have been able to pay full attention to each event. But for a fair test of the counterhypothesis, one would prefer a setting where the first observation is rather thorough, a setting where one can be more certain that most of the events are really observed at the first presentation. Therefore, the following two experiments use a different, slower display.

CONSECUTIVE PK EFFORTS BY TWO SUBJECTS

(EXPERIMENTS 2 AND 3)

The following two experiments were identical in design. Two subjects made consecutive PK efforts on the same prerecorded targets. As in the previous experiment, I acted as PK subject because no other promising scorer was available. The role of the second subject, the "control subject," was played in the two experiments by a 27-year-old woman and a 24-year-old man, respectively, neither of whom had shown promising scores in preliminary tests with the set-up to be used.

The tests were arranged so that sometimes the test subject and sometimes the control subject made the first PK effort. And sometimes the two efforts were in the same and sometimes in opposite directions. The subjects were kept ignorant of these conditions.

Prerecording the Random Events

For each of the two experiments, I filled a permanent memory chip (EPROM 2516, holding over 16,000 bits) with random numbers, using the same method as in the previous experiment. From this chip, a section of 10,240 bits provided the 80 test sections, numbered 1 to 80, with 128 bits in each section. The remaining bits were available for practice runs. The section to be used for the test runs was reshuffled with the help of random number tables as described in the first experiment. Each section was used twice, for one run with the test subject and for one run with the control subject.

Computer Feedback in a Test Session

I used a small computer with TV display (RCA COSMAC, VIP), programmed in machine language for the RCA CDP 1802 microprocessor. I modified the computer by the addition of a permanent program memory so that the system was always ready for an experiment, without the need of loading a program first. The computer is no longer available, but with the following information the reader might adjust the program to other computers.

The display was provided by a pendulum on a TV screen, swinging with randomly changing amplitude, with a typical frequency of one cycle per second. The pendulum could swing with seven different amplitude values, 1,2,...,7. After each half-cycle, the computer read the next of the 128 bits used for a run. In the "normal mode," a 1 increased the amplitude by one step, or left it unchanged at the maximum value. A 0 decreased the amplitude by one step or left it at the minimum value. This arrangement guaranteed that the amplitude changes occurred gradually. The score of a run was defined as the sum of the amplitude values assumed at the 128 steps. If a run is always started with the medium amplitude value of 4, the average score is:

Score average = 512.

The variance is not as easily calculated. To determine this value, I generated (with the true random number generator mentioned) a total of 1,024 runs. This gave an average value for the run variance of:

Score variance (sigma) = 95.8.

The protocol for each subject specified a high score as PK target for half the runs and a low score for the other half. But since the PK subjects preferred small amplitudes as goal, an inverter switch was provided. With this switch in the "invert" position, the role of the 1's and 0's was interchanged. Now the 0's increased and the 1's decreased the displayed amplitude. When the protocol called for high scores, the subject could flip the switch and then aim for low scores, because now high scores corresponded to low average amplitudes.

Test Assignments for the Two Subjects

The two participating subjects, the test and the control subject, worked at home using identical computers with identical memory chips. Each subject was provided with an assignment list specifying the sequence in which the 80 sections should be used and the target direction for each section. To provide for the correct relative timing of the two PK efforts, I grouped the runs in blocks of eight runs, and the assignment list specified in which time slot (usually a two-day period) each group had to be completed. To prevent rushing a subject who might not always feel in the right mood for the tests, the time slots for both subjects could be easily rescheduled.

This arrangement guaranteed the following:

1. Each of the 80 test sections was subject to two PK efforts. Half of these efforts from the two subjects were in the same direction and the other half in opposite directions.

2. In half of the runs in each group, the test subject was the first to make the effort, and in the other half, the control subject.

3. The subjects never knew whether the two efforts were in the same direction or in opposite directions. And with the exception of the first four and the last four runs, the subjects did not know whether the present effort was the first or the second PK attempt at this binary sequence. (The details of the arrangement are given in Appendix B.)

Test Sessions and Results

Each of the two experiments was conducted within a 3 weeks' time span, in February and March of 1984. I had decided in advance to base the final conclusions (with regard to the null hypothesis to be tested) on the performance of the test subject only, because neither of the control subjects had previously shown interesting scores. In reading the results, remember that each experiment used 80 sections of 128 bits, which were displayed, with identical or opposed target directions, to the two subjects. Sometimes one and sometimes the other subject made the first PK effort.

Depending on the PK efforts made, the 80 strings fall into four categories of 20 strings each. I define the scores (deviations from chance) for these categories as follows:

S[T,C] = S1: Score of T for the 20 sections where T made the first effort and C made the second effort in the same direction.

S[T,-C] = S2: Score of T on the 20 sections where T made the first effort, and C made the second effort in the opposite direction.

S[C,T] = S3: Score of C on the 20 sections where C made the first effort and T made the second effort in the same direction.

S[C,-T] = S4: Score of C on the 20 sections where C made the first effort and T made the second effort in the opposite direction.

TABLE 1

SCORES (DEVIATIONS FROM CHANCE) FOR THE FOUR CLASSES IN THE TWO EXPERIMENTS (Exps. 2 AND 3)

Class	Score	Exp. 2	Exp. 3
[T,C]	S1	751	439
[T,-C]	S2	438	1,027
[C,T]	S3	-121	226
[C,-T]	S4	152	535

Note: The variance for each entry is sigma'=428.

Table 1 lists the values obtained in the two experiments. I used the previously given value of sigma = 95.8 for the standard deviation per run. The standard deviation for each entry in the table is therefore:

sigma' = sigmasqrt*(20) = 428.

In interpreting the result with regard to the null hypothesis, consider the scores of the test subject T in the two situations, where he is the first or the second to make the PK attempt. The score deviation obtained by T in these two cases can be written:

S(T=first) = S[T,C] + S[T,-C] = S1 + S2.

S(T = last) = S[C,T] - S[C,-T] = S3 - S4.

Note that C made equal numbers of efforts in both directions, so that a possible PK effect by C could not lead to a bias of the total score of T in one or the other direction.

We count the scores always as positive if the first subject succeeds. Since in the last case the two subjects have opposite goals, success by T implies failure by C and a correspondingly negative S4 value.

Under the null hypothesis, the time sequence of the two PK efforts should not matter; that is, T should get the same scores, no matter whether the effort by C is made earlier or later.

The counterhypothesis, in its most extreme form, implies that T cannot have PK success if the trials have been already worked upon (and observed) by C; that is,

S(T = first) = S (T = last) (null hypothesis)

S(T = last) = 0. (Counterhypothesis)

To test the null hypothesis, therefore, I considered the difference:

Diff = S(T=first) - S(T=last)= S1 + S2 - S3 + S4.

The two experiments give for the differences and for the corresponding Z values:

Diff(2) = 1462, Z(2) = 1.7

Diff(3) = 1775, Z(3) = 2.1.

The positive values of these two differences both speak against the null hypothesis.

Figure 1 gives the cumulative scores for the combined two experiments under the two conditions where (a) the PK subject was the first observer or (b) the prerecorded data had been previously observed by the control subject. The first case gives a rather steady increase of the cumulative score (deviation from chance expectancy), leading to a total Z value of 3.1. But the second case shows no significant PK effect (Z = -0.7).

The calculation of the Z values was based so far on the experimentally determined standard deviation (sigma=95.8) for the individual run. The fact that the run scores might not have a perfect normal distribution seems to present no problem because a large number of individual runs contribute to the final scores. As a double check, however, I recalculated the Z score for the upper curve in Figure 1, using a nonparametric method (rank order test), which makes no assumption about the distribution. Because I had reshuffled the first random numbers generated, the method protects against even malfunctions of the random number generator. This conservative method gives a value of Z=3.15, very close to the one provided by the simpler method (3.10).

CONCLUSION

The three experiments were specifically designed to test the following null hypothesis:

If two PK efforts, A and B, are made on the same prerecorded random events, and if the subjects are blind to the test conditions, then the scores are independent of whether the effort A or B comes first.

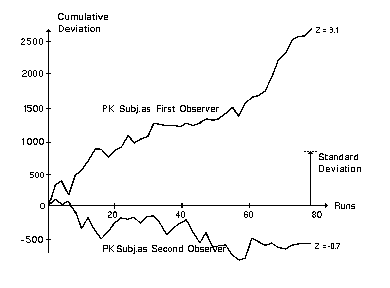
Figure 1. Combined result of the two experiments in which a PK test subject and a control subject made consecutive PK efforts on the same prerecorded sequences. In the half of the runs, where 1, the test subject, was the first to see the prerecorded random events, my cumulative PK score increased regularly (upper curve). But in the other half, where the control subject had seen the events first, my PK effort was no longer successful (lower curve).

Each of the three experiments measured a random variable that, under the null hypothesis, has normal distribution with zero mean.

All three experiments gave positive values for this variable - Z(1)=0.71, Z(2) = 1.70, and Z(3) = 2.07 - which can be combined to a total Z value:

Z(tot) = [Z(1) + Z(2) + Z(3)]/sqrt(3)= 2.59.

This result rejects the null hypothesis with odds against chance of 50:1.

The theoretical model associated with the null hypothesis (Schmidt, 1975) seemed attractive insofar as it emphasized the space-time independence of psi and showed a close link between PK and ESP effects. On the other hand, the model implied an annoyingly large effect of future observers on the outcome of a present experiment, which found its mathematical expression in the "divergence problem" (Schmidt, 1975). If the null hypothesis is wrong, as our experiments indicate, we can stop worrying about the divergence problem.

The result suggests that the first PK effort has a stronger, or even the only, effect on the outcome, as if the first observation of the scores would lock in the result, blocking all further PK efforts.

Taking the quantum collapse model seriously, one would say that the first observation collapses the wave function, forcing nature into a fully determined state that leaves no room for PK effects.

This model (Schmidt, 1984) allows for a partial collapse of the wave function if there was not sufficient time for the subject to fully absorb the feedback information, as might have been the case in our first experiment. Such a partial collapse of the wave function could also explain why in an earlier study (Schmidt, 1976) with high-speed feedback, repeated PK efforts on the same targets could lead to higher scores.

Certainly, there is no claim that the results "prove" the quantum collapse model. There may be many models consistent with the reported results. In particular, one might be concerned that an experimenter with theoretical expectations might use a global, goal-oriented PK mechanism to adjust the total outcome to his expectations. Thus, replication or extension of the results by other researchers will be most important. And there are still many interesting questions open for study: Does the first observer's mental state make a difference? Does he have to be alert, does he have to care about the outcome? Does the observer have to be human, or could a cat or a goldfish as observer also collapse the wave function?

An exploratory study with a dog as the first observer was reported previously (Schmidt, 1984), but more extensive experiments are necessary.

APPENDIX A

ENCODING OF THE RUN ASSIGNMENTS IN EXPERIMENT 1

For a run number (1 to 40), an encoded run number n' was obtained through the relationship:

n' = n + 151 RN*

with an integer random number (RN) in the range from 0 to 430. To disguise the number even more, I printed it as a 4-digit hexadecimal number, to be entered by the subject at the run start. In this manner, two generally very different encoded numbers were associated with the same binary sequence so that the subject could not notice the connection. To decode the encoded number, the computer simply had to subtract as many multiples of 151 as necessary until a number in the range between 1 and 40 was obtained.

To prepare the list with the encoded run numbers and associated settings (UP or DOWN) of the assignment switch, I used the following steps:

1. I had my ATARI computer print 40 lines, corresponding to the 40 run pairs. On the left side of each line was printed one encoding of the run number followed by the instruction UP. On the right side, was another encoding of the run number, followed by the instruction DOWN. I cut the printout into 40 strips of paper and shuffled the strips (with the help of random number tables plus ordinary shuffling methods). Now each strip contained two assignments for two paired runs.

2. I arranged 20 cups, numbered 1 to 20, in a circle and placed run assignments into them as follows:

I randomly selected one paper strip, cut it in the middle, and put one randomly chosen side into Cup 1 and the other into Cup 2. Similarly, I split the next strip (i.e., the run pair) between Cups 2 and 3, the next between Cups 3 and 4, and so forth, going twice around the circle until all pairs were distributed.

3. To get the assignment sequence for the experiment, I now randomly drew assignments in this sequence: two slips from Cup 1, all four slips from Cup 2 and so on, to all four slips from Cup 20, and the remaining two slips from Cup 1. I glued the slips in the proper order on a sheet of paper. This was the list specifying the sequence of run assignments that 1, the subject, used during the experiment.

Then, except for the two first and the two last runs, I never knew whether a run presented the first or the second effort at a binary sequence. Consider the assignments from Cup 10, for example. Two of the assignments had their twins in Cup 9, that is, they corresponded to second PK efforts. But the other two assignments presented first efforts, because their twins were in Cup 11, to be worked on later.

APPENDIX B

RUN ASSIGNMENTS FOR EXPERIMENTS 2 AND 3

The following procedure was used, with the help of an assistant.

1. For each of the subjects (T and C), 11 envelopes were prepared. The envelopes were labeled T0,...,T10 and C0,...C10.

2. Eighty strips of paper were prepared with the corresponding run number (1,...,80) printed on each end. These strips were shuffled and divided into 20 groups of four strips.

3. The four strips in each group were marked on each side with a target assignment, H or L, so that each of the four combinations H-H, H-L, L-H, L-L occurred once in each group. Then each strip contained two target assignments.

4. For the following 10 steps, n=0,1,...,9, this procedure was followed: (a) A group of four strips was randomly selected, cut in the middle, and divided between envelope Tn and C(n+1), so that one envelope received the four assignments from the right halves and the other the rest. Similarly, a group of four strips was divided among the envelopes Cn and T(n+1). (b) In this manner, each of the Envelopes 1 to 9 received eight assignments, and the Envelopes 0 and 10 got four assignments each. Then, from the assignments in Envelope T5, for example, four assignments had their twin (using the same binary sequence) in Envelope C4, and the rest had their twin (with the same binary sequence) in C6.

For the proper timing of the PK efforts, both subjects began with the assignments in their Envelope 0. And then a subject was permitted to proceed to the assignments in Envelope n+1 only after both subjects had completed their envelope number n.

REFERENCES

SCHMIDT, H. (1975). Toward a mathematical theory of psi. Journal of the American Society for Psychical Research, 69, 301-319.

SCHMIDT, H. (1976). PK effect on prerecorded targets. Journal of the American Society for Psychical Research, 70, 267-29 1.

SCHMIDT, H. (1977). A simple random number generator for use with minicomputers. Journal of the American Society for Psychical Research, 71, 17 1

SCHMIDT, H. (1984). Comparison of a teleological model with a quantum collapse model of psi. Journal of Parapsychology, 48, 261-276.

SCHMIDT, H. (1984). Superposition of PK efforts by man and dog. In R.A. White and R.S. Broughton (Eds.), Research in parapsychology 1983 (pp. 96-98). Metuchen, NJ: Scarecrow Press.

Mind Science Foundation
8301 Broadway, Suite 100
San Antonto, TX 78209