Recently, while in Mexico at the classic Maya site of Palenque, I made the aquaintance of a young British mathematician and psychokinesiologist named Matthew Watkins. Watkins offered the strongest and most interesting critique of the timewave and the assumptions of its construction yet made. Watkins is confident that he has condensed the theory of the timewave into a formula (given below) and is further convinced that there is no rational basis for assuming that the timewave represents the fluctuation of any quantity which can be meaningfully understood as "novelty". Here in Watkins' own words is his formula and his objection:
I first became aware of the Timewave theory when I discovered a magazine article on Terence McKenna four or five years ago. It briefly mentioned that he had developed a theory which involved mathematically modelling the historical ingression of "novelty" using a fractal generated from the King Wen sequence of I Ching hexagrams. The idea had been revealed to him whilst in an altered state of consciousness brought about by psilocybin mushrooms. I had been studying the I Ching for some time, was working on a PhD in mathematics, and had occasionally contemplated the role of psychoactive plants in ancient religious belief systems, so I was immediately fascinated and searched everywhere for more information. I discovered McKenna's writings and recordings, but although the theory was often referred to and used as a basis for some remarkable speculation, I was unable to find any detailed description of its foundations. Such a description had originally been published in The Invisible Landscape (Terence and Dennis McKenna) in the early seventies, an obscure book long out of print and almost impossible to find.
When, in 1994, I discovered that The Invisible Landscape had been republished, I immediately obtained a copy and studied it thoroughly. I was rather disappointed to find that the mathematical process which was applied to the King Wen sequence to generate the fractal "timewave" seemed worryingly arbitrary (no justification being given for many steps) and mathematically clumsy. Beyond that, the described procedure fails to give the same "data points" which appear in the appendix and which are used to ultimately define the fractal in question. More disappointing, I discovered that the December 21, 2012 date (now generally associated with McKenna's name) was in no way calculated - it was selected to give the timewave the "best possible fit" with the historical occurence of novelty as McKenna sees it. It was difficult to accept that such an exotic, imaginative idea could have such unsatisfactory foundations. I thought that perhaps McKenna had been unable to effectively communicate something very real which had been revealed to him, and decided to get in touch immediately.
We began an e-mail dialogue about a year ago, after he responded to a letter I sent offering mathematical advice (at this point I had completed my PhD on hyperspatial embeddings of differential manifolds). Little was achieved for many months. He referred to an idea he was exploring which related the distribution of large prime numbers to the timewave, but it was only when I received a copy of the Timewave software that I was able to look into this. I was unable to find any evidence to support the hypothesis, but I did find that the software manual gave a much more detailed account of the construction of the timewave than The Invisible Landscape had. The manual contained the actual source code which the software uses, so I was able to study it with great care and formulate a detailed critique of the theory. We agreed to meet and discuss the issue in Palenque (in the Mexican state of Chiapas) in January, while he was teaching at a Botanical Preservation Corps conference.
Terence and I had four lengthy, good natured, and most enjoyable discussions during the week I was in Palenque, and I was able to explain my critique step-by-step. By the final discussion he seemed to have fully grasped the nature of the problem, and had admitted that the theory appeared to have "no basis in rational thought". He claimed (and this struck me as sincere) that he was only interested in the truth, and that someone "disproving" the theory was just as a much of a relief to him as someone confirming its validity. He proposed that we collaborate on a piece provisionally entitled "Autopsy for a Mathematical Hallucination" in which we would carefully take the theory apart and see what had gone wrong. He claimed that I was the first person to approach him with a serious mathematical critique of his ideas, partly explaining why such an unjustifiable theory had not only survived for so long, but also attracted so much interest and attention.
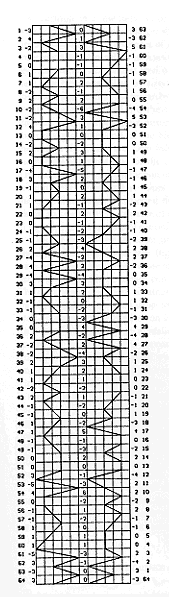
The timewave is a mathematical function defined by applying a "fractal transform" to a piecewise linear function. The latter function is an expression of 384 "data points" (positive integer values) derived from the King Wen sequence. Strangely, McKenna's description of the derivation in The Invisible Landscape fails to yield the data points which appear in the appendix and which have been used since. However, a complete description can be found in the TimeExplorer software manual. With some effort, the multi-step description, largely expressed in graphical or intuitive terms, can be condensed into a single formula.
We define a set of 64 values h[1], h[2],..., h[64] such that h[k] is the number of lines which must be changed in hexagram k to give hexagram k+1. Here "hexagram 65" is interpreted as hexagram 1, "hexagram 0" as hexagram 64, etc. These values are as follows:
h[1]:=6; h[2]:=2; h[3]:=4; h[4]:=4; h[5]:=4; h[6]:=3; h[7]:=2; h[8]:=4;
h[9]:=2; h[10]:=4; h[11]:=6; h[12]:=2; h[13]:=2; h[14]:=4; h[15]:=2;
h[16]:=2;
h[17]:=6; h[18]:=3; h[19]:=4; h[20]:=3; h[21]:=2; h[22]:=2;
h[23]:=2; h[24]:=3;
h[25]:=4; h[26]:=2; h[27]:=6; h[28]:=2; h[29]:=6;
h[30]:=3; h[31]:=2; h[32]:=3;
h[33]:=4; h[34]:=4; h[35]:=4; h[36]:=2;
h[37]:=4; h[38]:=6; h[39]:=4; h[40]:=3;
h[41]:=2; h[42]:=4; h[43]:=2;
h[44]:=3; h[45]:=4; h[46]:=3; h[47]:=2; h[48]:=3;
h[49]:=4; h[50]:=4;
h[51]:=4; h[52]:=1; h[53]:=6; h[54]:=2; h[55]:=2; h[56]:=3;
h[57]:=4;
h[58]:=3; h[59]:=2; h[60]:=1; h[61]:=6; h[62]:=3; h[63]:=6; h[64]:=3;
h[0]:=3;
The formula for the values w[0], w[1],..., w[383], the 384 "data points" which lie at the heart of the entire timewave construction, can be expressed in the popular mathematical programming language MAPLE as follows (Peter Meyer has written a conversion to C):
w[k] := abs( ((-1)^trunc((k-1)/32))*Here trunc represents trunctation (rounding a number down to its integer part), abs means absolute (positive) value, and mod 64 means "the remainder after dividing by 64". Of this formula, McKenna writes:
Naturally [it] is of interest to myself, Terence McKenna and to others, especially Peter Meyer and other mathematicians and computer code writers who have help to advance and formulate the theory of the timewave over the years. On March 25, '96 Peter Meyer sent me e-mail which contained the following statement: "I have tested it (the formula) and have the pleasure of reporting that the formula produces correct values. I have congratulated him by e-mail." As of April 1, 1996 Watkins has significantly advanced understanding of the timewave by writing the formula that has eluded other workers since 1971.Although I was happy to have clarified the issue, I am unaware of any one else who had attempted to find such a formula. It was no great feat, being merely the compression of a step-by-step computer algorithm (as given by Peter Meyer in the TimeExplorer software manual) into a single mathematical expression, something which any competent mathematician could achieve with relatively little effort.
Now we must change the sign of half of the 64 numbers in angle_lin[] as follows
For 1 <=j <=32
angle_lin[j]=-angle_lin[j]
When reading this, I immediately thought "WHY?", as did several friends and colleagues who I guided through the construction. There is no good reason I could see for this sudden manipulation of the data. Without this step, the powers of -1 disappear from the formula, and the "data points" are a different set of numbers, leading to a different timewave. McKenna has looked at this timewave and agree that it doesn't appear to represent a map of "novelty" in the sense that the "real" timewave is claimed to. It is possible that by changing the "zero date" Dec. 21, 2012, one could obtain a better fit, but there's no longer any clear motivation to attempt this, as the main reason for taking the original timewave seriously were McKenna's (often very convincing) arguments for historical correlation. These would all be rendered meaningless without the aforementioned step.
The footnote associated with this step reads:
22. This is the mysterious "half twist". The reason for this is not well understood at present and is a question which awaits further researchThis struck me as absurd. After all, why introduce such a step into an (already overcomplicated) algorithm whilst admitting that the reason for doing so is "not well understood at present"? I confronted McKenna on this issue, and he immediately grasped the significance of my challenge. He would have to either (1) justify this mysterious "half twist" or (2) abandon the timewave theory altogether.
He claimed not to remember the exact details for its inclusion, as it had been decided upon over 20 years ago. After some time, he pointed out the antisymmetry which occurs in the central column of values in the figure below:

Having conceded that the above doesn't constitute a justification of the "half twist", McKenna went on to claim that without it the collapse of the "multi-levelled complex bi-directional wave" into the 384 values "fails to preserve" some geometric property. The "collapse" is pictured in the figure below:
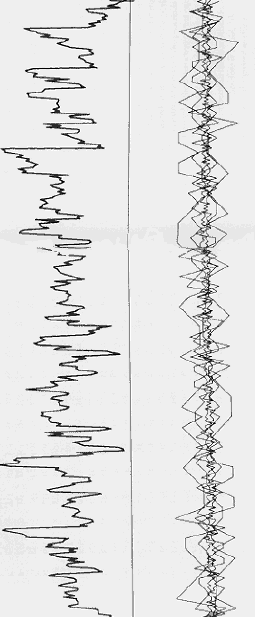
I'm now in the slightly awkward position of having to use mathematical reasoning to disprove an assertion which hasn't actually be stated in mathematical terms, but which is obviously mathematical in content. There is no doubt that McKenna's timewave is a well-defined (if irrelevant) mathematical function, but any considerations of its interpretation lie ouside the domain of mathematical logic. We must therefore take into account McKenna's argument for the "half twist", for if he as no good argument (as the footnote originally suggested), even he agrees that the theory can no longer be taken seriously.
We first note that the formula consists of the sum of two positive values:
w = |angular term| + |linear term|
((-1)^[(k-1)/32])*
((h(k-1 mod 64) - h(k-2 mod 64)) - (h(1-k mod 64) -
h(-k mod 64)))
+ 3*((-1)^[(k-3)/96])*
((h([k/3]-1 mod 64) - h([k/3]-2 mod
64)) - (h(1-[k/3] mod 64) - h(-[k/3] mod 64)))
+
6*((-1)^[(k-6)/192]*
((h([k/6]-1 mod 64) - h([k/6]-2 mod 64)) - (h(1-[k/6]
mod 64) - h(-[k/6] mod 64)))
Now the "multi-levelled bi-directional wave" shown on the right hand side of
Figure 2 (above) is actually the superimposition of six piecewise linear
functions defined over the interval [0,384]. These functions are built from the
two halves of Figure 1 (above). McKenna refers to these as (left) the forward
flowing wave and (right) the backward flowing wave. Our six functions
are:
The "angular term" mentioned above is essentially a weighted sum of the relative slopes of the three pairs of resonances. We can rewrite it as
(-1)^[(k-1)/32]*(forward yao slope at k - backward yao slope
at k)
+ 3*(-1)^[(k-3)/96]*(forward tri slope at k - backward tri slope at k)
+ 6*(-1)^[(k-6)/192]*(forward hex slope at k - backward hex slope at k)
Without the powers of (-1), which are a direct consequence of the "half twist", we would have something which could be considered an expression of the local geometry of the "6-levelled object" at k. These powers modify the three contributions in a k-dependent way. Consider the following table:
Sign of contributions for yao resonance term
1 <=k
<=32 : +
33 <=k <=64 : -
65<=k <=96 : +
97<=k
<=128 : -
129<=k <=160 : +
161<=k <=192 : -
193<=k
<=224 : +
225<=k <=256 : -
257<=k <=288 : +
289<=k<=320 : -
321<=k<=352 : +
353<=k<=384 : -
Sign of contributions for trigrammatic resonance term
1<=k<=2 : -
3<=k<=98 : +
99<=k<=194 : -
195<=k<=288 : +
289<=k<=384 : -
Sign of contributions for hexagrammatic resonance term
1<=k<=5 : -
6<=k<=197 : +
198<=k<=384 : -
So we see that the value of w(k) cannot be determined from the local geometry of the six-levelled object in a neighbourhood of k. The "collapse mechanism" built into the formula is clearly k-dependent. Therefore we see that not only is the inclusion of the "half twist" failing to guarantee the "preservation" of some geometric property to which McKenna has referred, but the failure is precisely because of its inclusion. McKenna's stated reason for this (crucial) step of the construction is unacceptable. As a mathematician who has met and talked with him, who is sympathetic with the majority of his other work, and who is only interested in spreading clarity, I must conclude that the "timewave" cannot be taken to be what McKenna claims it is.
On a more positive note, I should add that I don't find McKenna's timewave exploit to be completely without value. Certain observations (such as the absence of 5's in the set {h(1),...,h(64)} and the correspondence of the Chinese 13-lunation ritual calendar with six 64-day cycles) are certainly worthy of further consideration. It wouldn't surprise me if a fractal map of temporal resonance was encoded into the King Wen sequence, just as it wouldn't surprise me if something quite remarkable does occur on December 21, 2012. The world can be a very strange place, and we all have much to learn. McKenna's hyper-imaginative speculation has fired the imagination of many. With this particular "theory" he has spread awareness of the I Ching and the Mayan calendar, both fascinating and poorly understood systems of ancient human thought. I should therefore end by suggesting that the remainder of his published thought should not be dismissed as a result of my findings which are discussed here.
Terence McKenna died April 3, 2000.
Gyrus - "The End of the River" (highly recommended)
"A critical view of Linear Apocalyptic Thought, and how Linearity makes a sneak appearance in Timewave Theory's fractal view of Time..."
 RetroPsychoKinesis Project
Home
RetroPsychoKinesis Project
Home