by John Walker
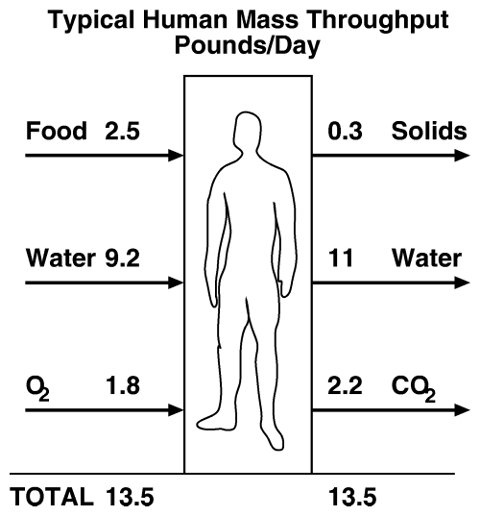
Some time ago, a reader of my book, The Hacker's Diet, wrote with a query about the following illustration, adapted from a NASA presentation on life support requirements for a manned mission to Mars.
The reader observed that since the mass-in and mass-out were the same, it appeared the human body was a perpetual motion machine: where did the energy it consumes come from? This energy is substantial. Human energy consumption varies from person to person according to their size, metabolic rate, degree of physical activity, and environmental conditions. A small adult with little physical activity might consume around 2000 kilocalories (kcal) per day. (Confusingly, nutritionists often call kilocalories, the most common unit for food energy, “calories”. This is sloppy and sometimes confusing. It's done because if you use actual calories [the amount of energy required to heat one gram of water one degree Kelvin], the numbers become unwieldy—around 50,000 calories in an Oreo cookie. So instead, they say it's 50 “Calories”, meaning 50 kilocalories, where a kilocalorie is 1000 calories, or the energy required to heat a kilogram [about one litre] of water one degree Kelvin.) Military combat rations in Meal, Ready-to-Eat form provide around 3600 kcal per day, while rations for explorers doing strenuous work in polar climates range up to 6500 kcal per day. The body burns a great deal of energy simply maintaining its temperature: if you want to lose weight quickly, take a job in a meat locker.
Let's assume human metabolism requires about 2000 kcal per day, because this is both typical of the lifestyle of many people in the developed world and is the reference used in nutritional labels for percentage of daily requirement. As a unit of energy, we can convert 2000 kcal to watt-hours, yielding 2324. Dividing this by 24 hours in a day, we find the human body, not doing strenuous exertion and in normal ambient temperature, expends around 97 watts—let's call it a hundred.
So, where does that energy come from, and why doesn't it show up in the chart?
Special relativity!
No, really! The calories extracted from the inputs, used to power the body's functions, and ultimately radiated away as heat to the environment are generated by chemical reactions (in most cases mediated by biological enzymes) which transform the inputs into the outputs, liberating energy in the process. As a result, the outputs contain less free energy than the inputs, because they have replaced the reactants with the products of the reaction.
Now, this energy release was done by rearranging atoms from a form with more free energy to less, precisely as happens in a less subtle form when you burn coal in oxygen to yield ash, CO2, and energy. In both cases, if you weigh the outputs you'll discover they weigh the same as the inputs, because mass is conserved.
Well, up to a point, Lord Copper. Actually, since the chemical binding energy has been released, there is less of it in the output than in the input, and as Einstein explained, that's equivalent to mass. But the quantity is so small (because the square of the speed of light is so large) that for almost all practical purposes it can be neglected. For example, plugging in 2000 kcal into good old E=mc² we find that the outputs from a day's bodily metabolism will mass 93.1 nanograms less than the inputs due to reduced binding energy. My scale doesn't read to that precision.
We usually think about the interconversion of mass and energy in connection with nuclear reactions, because that's where it is most apparent, but it is a general phenomenon. For example, if you heat a litre of water from near freezing to near boiling temperature, the random jiggling of the water molecules will increase in velocity (which is precisely the definition of heat). This motion, according to Einstein's equation:
will cause a small increase in the mass of the water and, in the Earth's gravitational field, its weight. How much? Well, a litre of water is about a kilogram, so to heat it from 0° C to 100° C will require 100 kcal of energy (about two Oreo cookies), which will increase its mass by 4.66 nanograms. This is a tiny value, but comparable to the mass of four average human cells.
|
|
This document is in the public domain.