« Fourmilab: New In-house Server in Production |
Main
| Home Planet Version 3.3RC1 Now Available »
Tuesday, August 8, 2006
Mathematics: Zipf's Law and the AOL Query Database
You may have heard about the most recent
scandal at AOL, which compiled a statistical sampling of more than twenty million search terms entered by more than 650,000 of their trusting customers, and then made this database available to the public for research purposes. While user names were replaced by numbers, these numbers provide a “thread” by which queries by a given user may be identified so that if, for example, a user entered some piece of information which permits their identity to be discerned, all the other queries they made during the sampling period may be identified as theirs.
AOL have admitted that this wasn't, even by AOL standards, such a bright thing to do, and have pulled the database from their “research.aol.com” site (the very domain name almost tempts one to chuckle), but one of the great problems or strengths of the Internet, depending upon whether you're the one who has made a tremendous goof or everybody else looking to exploit it, is that it's essentially impossible to “un-publish” something once it gets loose in digital form. While AOL have deleted the file, it has already been mirrored all over the world: here is a
handy list of places in case you're interested in getting a copy for your own research. (Note: even as a Gzipped TAR file containing individually Gzipped text files, this is a 440 megabyte download; if you don't have a high-speed Internet connection, or you pay by the amount you download, this probably isn't for you.) Well, I do have a 2 Mbit/sec leased line which is almost idle in the inbound direction, so I set my development machine downloading this file overnight, and by the crack of noon it had arrived
chez moi.
The first thing I wanted to look at was, as you might guess, the most popular search terms. I wrote a little Perl program which parsed the query strings from the records, divided them into words, and computed a word frequency histogram. Here are the most common twenty words in queries from the database, with the number of occurrences in the complete list of 36,389,567 records:
| 1 | com | 5,907,621 |
| 2 | www | 3,618,471 |
| 3 | of | 1,127,393 |
| 4 | in | 946,216 |
| 5 | the | 848,407 |
| 6 | for | 699,547 |
| 7 | and | 693,682 |
| 8 | google | 543,052 |
| 9 | to | 473,015 |
| 10 | free | 460,569 |
| 11 | s | 448,308 |
| 12 | yahoo | 416,583 |
| 13 | a | 403,375 |
| 14 | myspace | 364,657 |
| 15 | org | 336,277 |
| 16 | new | 273,897 |
| 17 | http | 269,856 |
| 18 | on | 256,646 |
| 19 | pictures | 240,376 |
| 20 | county | 234,618 |
This isn't at all what I would have guessed, but of course after a moment's reflection, you realise
these are AOL customers—they type URLs (with their elbows, no doubt) into the
search box, not the URL field! Since inquiring minds need to know and will doubtless send me feedback to ask, “sex” is number 27, “nude” 50, “porn” 65, “science” 503, “freedom” 2537, “democracy” 11337, and “libertarian” 36334—
welcome to the monkey house!)
Next, as I am wont to do when presented with a large corpus of primate-generated text, I wanted to see how well
Zipf's Law (or, more generally, the observation that the relation between the rank of items by frequency and the number of occurrences in real-world collections is almost always closely approximated by a power law). Given the query word frequency table, it was easy to perform this analysis: I just dug out the program I'd written for the study which appears on pages 339–346 of
Rudy Rucker's
The Lifebox, the Seashell, and the Soul. A little twiddling and fighting with the hideously opaque charting facilities in OpenOffice Calc yielded the following plot:
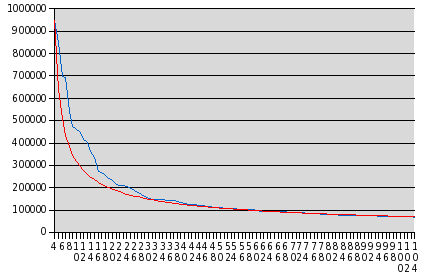
The
X axis (with the numbers reading vertically down) is the rank of a given word in the frequency list, while the
Y axis gives the number of times that word appeared in the collection of queries. I dropped the three most common words in the list as “outliers”, which would distort the overall curve. The blue line shows the actual relationship in the database. The red line is a plot of the empirically determined function:
y = 946216 / ((x − 3)0.56)
Power laws
rule! Now while the exponent in this relation differs a great deal from the pure inverse relation Zipf observed for English text, it is clear that word frequency in the very different dialect of search requests is still closely modeled by a power law distribution. It's interesting to speculate what the exponent has to say about the vocabulary of the corpus of text whose distribution it best models. And wouldn't you just
love to know the exponent which best fits the queries of other search engines?
Update: Joe Marasco (
read his book) wrote to complain that my discarding the three most frequent words in the plot above as “outliers” invalidated the Zipf's Law analysis since, as he observes, one of the most remarkable things about the relation is how well it fits the most common words, not just the tail of the distribution. Well, actually, I did not exclude the three top words because they don't fit the distribution, but simply to make the chart easier to read. Including the top word, “com”, which occurs almost six million times in the database, causes the chart to be scaled so that most of the detail is difficult to see. The fit is arguably
better if the top three words are included, as you can see in the following plots:
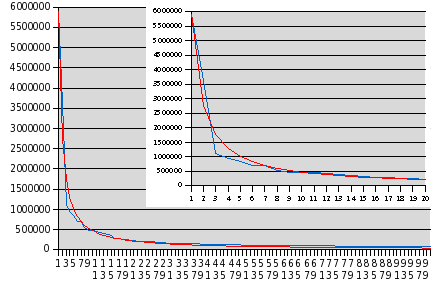
The blue line is the actual frequencies of the top 100 words and the red line is the fit by
y = 5907621 / (x1.1).
Note that in this case the exponent of 1.1 is much closer to the value of unity in Zipf's law for English text. I have inset a plot for just the first twenty words, which makes the fit for the most common words easier to evaluate. (2006-08-09 18:05 UTC)
Posted at August 8, 2006 21:38

