Abstract- This paper discusses evidence for a psychokinetic effect acting on chance events. Emphasis is laid on psychokinetic action on pre-recorded random processes and its interpretation in terms of two general hypotheses, the weak violation hypothesis, and the equivalence hypothesis. These hypotheses imply that psychokinesis can act on the outcome of indeterministic quantum events only, and that, basically, all such events are affected to the same degree.
Most of this paper will emphasize the interesting, challenging aspects of parapsychology, pointing out how a study of psychic effects may lead to a more fundamental understanding of nature, and perhaps of quantum theory. Indeed, parapsychology appears as a dynamically progressing field of research. Good statistical methods for observing the effects in the laboratory have been developed. Modern electronics has been utilized to gather data efficiently and reliably, and even though there is not yet a final theory, there are theoretical models to provide a lively interaction between ongoing experiments and theoretical ideas.
And yet, there are a number of disquieting questions, ranging from very practical matters to basic conceptual issues. Most perplexing for the experimenter is the elusive nature of the phenomena. Although the results are too persistent and statistically too significant to be seen as mere flukes of chance, it is often difficult to replicate previous results on demand (Edge, Morris, Palmer, & Rush, 1986).
One may argue that psychic performance, like creativity, depends on subtle psychological factors that are difficult to identify and to control; and one may expect progress from ongoing experiments using motivational techniques, meditation methdds or electronic feedback devices to help the subject's mental effort.
On the other hand, the replicability problem may be deeply rooted in the exotic nature of the psychic mechanism. The experiments to be discussed will use the psychokinetic effect (PK) as an example to emphasize these conceptually perplexing features.
The psychokinesis experiments to be discussed developed out of Rhine's experiments with dice (Rhine, 1970; Rhine & Rhine, 1943). Rhine reported that some people could mentally influence the outcome of dice falls even when they had no physical contact with the dice. In this context, it does not matter whether Rhine's experiments were good or bad. What matters is that subsequent work with improved methods and new ideas has confirmed the existence of PK.
A great surprise of the early work was that PK affected only rolling dice, but could not be measured as a force acting on a stationary die on a sensitive scale. PK seemed to act only where chance processes were involved. This suggested that PK could not be considered as a force, comparable to electric or magnetic forces.
At the early stages of psychical research it seemed appropriate to introduce labels like telepathy, clairvoyance, precognition and psychokinesis to distinguish different psychic "mechanisms." Today, such a clear distinction between different psychic mechanisms seems impossible, experimentally as well as conceptually, because all our naive intuitive notions about the underlying mechanism seem misleading. It is still convenient to use some labels to specify experimental test arrangements. We will use the term psychokinesis, for example, to describe a setting where a subject mentally tries to affect the outcome of some random process. If there is an anomalous, persistent correlation between the subject's effort and the random events, then we will call this a PK effect. But it might be meaningless to argue whether the observed correlation was "really" produced by psychokinesis or some other psychic mechanism.
With PK acting on the outcome of dice falls, it seemed natural to explore PK action on other chance events, and in particular on the outcome of indeterministic quantum jumps. Beloff and Evans (1961) were the first to look for a PK effect on radioactive decays, without success. But a few years later Chauvin and Genthon (1965) reported success in a similar experiment, where the participants tried to speed up or slow down the counting rate of a Geiger tube.
Subsequently, a more stable and more convenient PK test arrangement came into use (Schmidt, 1970), based on a digital random generator. To obtain such an "electronic coinflipper," we can program a computer to count upward at a high rate of 100,000 or more steps per second, and make an arrangement such that the counting process is stopped whenever a signal from a Geiger tube is registered. With these signals arriving at truly random times, there is an equal probability for the computer counter to stop at an even or an odd number. Therefore, we obtain a truly random decision for even/odd or head/tail. This and similar devices have been used in much of the recent PK work.

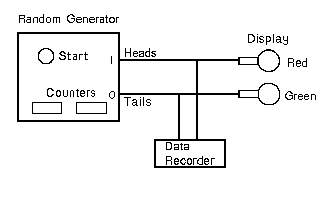
Fig. 1. Test arrangement for a psychokinesis experiment
Figure l shows the setup for a typical PK experiment. The box at the left contains the basic electronic coinflipper in combination with counters for the heads and tails. When a pushbutton is pressed, the system generates 128 binary decisions at the rate of one per second. The decisions are internally counted and transmitted through two output lines to an external recorder. A most simple display can be provided by a red and a green lamp, indicating the generated heads and tails respectively.
For a PK test, one instructs the subjects to concentrate, for example, on the red lamp, trying to make this lamp flash more often than the green one. This goal corresponds to an increased generation rate of heads. At the end, one can assess the success from the two counters and from the detailed external record.
For my own experiments, I found it inefficient to gather data from a very large number of unselected people because the poor scores of the majority tend to dilute the effect of the successful performers. Therefore, I pre-selected promising subjects, and then used these subjects immediately in a subsequent formal experiment with a previously specified number of trials. Unfortunately the process of locating and pre-selecting promising subjects is time consuming and often frustrating.
PK tests with binary random generators
Table 1 shows the result of my first experiment (Schmidt, 1971) with a group of 15 selected subjects. We see that 50.9% of the electronic coinflips went in the expected direction. With the large number of binary decisions involved, this small effect is statistically significant with odds against chance of 1000:1.
For my second experiment, I had found two unusually promising performers. The subsequent formal experiment could confirm their strange ability. With a scoring rate of 52.4% hits, the result is statistically significant with odds against chance of 10 million to one.
These results confirm the existence of PK as a weak but real effect. More details, including the precautions taken against errors are described in the references.
So far, 27 other researchers at many different institutions have published PK studies with binary random generators (Radin, May, & Thomson, 1985). The overall significance of these data appears high, but there may be a bias insofar as researchers with negative results might be less likely to publish their findings. Two of the studies may appear particularly interesting because they were conducted at well known laboratories.
Dean Radin (1981) at Bell Labs reported highly significant PK effects, using my equipment, which he had re-tested for randomness and reliability.
A large scale approach to PK was started by Robert Jahn at Princeton University (Nelson, Dunne & Jahn, 1984). Working with a limited number of unselected subjects, his group studies personal patterns in PK performance. The overall positive results suggest that, with psychologically skilled experimenters and sufficient patience, PK can be produced in a routine manner.
These results and the results to be discussed later leave, I think, no doubt that a PK effect exists, in discord to currently accepted laws of physics.
Certainly, the observed effects are disappointingly weak, so that it stil takes many man-hours to merely confirm the existence of PK.
This makes precise quantitative comparisons often impractical. If we want to compare, for example, the PK action in two different settings, then the number N of trials required to establish the existence of PK under one condition is already unpleasantly large. But if there were only a small, say 10%, difference in the PK action on the two systems, then we would need about 100 times N trials to establish this difference.
It remains to be seen whether, with increased research effort and growing theoretical understanding, the PK effects could be raised to a practically useful level.
For the moment, it seems best to postpone some detailed questions. If we find, for example, that PK works approximately equally well over large and short distances, we might bypass the enormous effort required for a high precision comparison and tentatively assume the simple hypothesis that PK is distance independent.
Similarly, I will introduce in the following two hypotheses that, so far, seem consistent with experimental results, but are open to future scrutiny by more precise measurements. These hypotheses stand out through their conceptual simplicity and their far reaching implications.
Laboratory experiments suggest that PK might violate the conventional laws of physics only in the weak sense in that only the outcome of chance processes is affected whereas the non-statistical laws of physics like the conservation laws for energy, momentum, symmetry, etc. are upheld.
The hypothesis of such a weak violation of conventional physics has great intellectual appeal; and it is a practically fruitful working hypothesis in stimulating new experiments.
If our world were governed by classical physics, with the motion of all atoms ruled by deterministic laws, then an element of randomness, and with it psychic effects, might enter only through the statistical initial conditions. We will not pursue this possibility, however, because, in the real world, quantum effects provide a new source of randomness. In the framework of quantum theory, the weak violation hypothesis can be interpreted in the sense that PK affect only the outcome of the random quantum jumps for which quantum theory makes no unique prediction. Such a hypothesis provides a specific link between PK effects and quantum theory, and leads to rather exotic implications.
Consider as example a situation, often discussed in connection with the Einstein-Podolsky-Rosen experiment, where we have two systems A and B that are quantum-correlated but spatially far apart. In the framework of quantum theory, the correlation between observations at A and B can not used for information transmission. Assuming, however, that we have a PK subject able to bias the outcomes of the A measurement on demand, the situation changes. According to the weak violation hypothesis, the correlation between the observations at A and B (which is given by a conservation law rather than a statistical law) is not affected by PK. Therefore, a PK induced bias in the events at A is instantly observable in a corresponding bias of the events at B. If the PK subject could still perform in such a setting, we would have an instant telegraph.
The beauty and also the technical difficulties of an EPR experiment lie in the fact that, before the measurement, the branches at A and B are still simply correlated (if we want, we can still observe interference effects). Barring nonlocal interactions, this supports the interpretation that the decision for the outcome of the A-measurement occurs only at the time of the observation, when the subject makes the PK effort.
One might wonder, however, whether the full EPR arrangement is necessary for PK success. If we need only quantum correlated and spatially far separated systems, we can provide that very easily. Consider the following nearly trivial case:
Let a quantum mechanical random generator make a decision to light a red or a green lamp, and let an automatic polaroid camera take two (identical) pictures of the resulting color. Without looking, insert the pictures into two envelopes to be mailed to distant locations A and B. Then the pictures at A and B are correlated: they both show a red or a green lamp.
The vital difference to the EPR situation is that, with the outcome of the random event macroscopically recorded on film, we can no longer observe an interference between the red and the green state. The previous argument that nature decides for the outcome only at the observation at A is no longer valid. But neither do we have solid support for the counter hypothesis that the decision for red or green is made before the human observation. If, therefore, we instruct a subject at A to open the envelope while wishing for a red color, this PK effort might still succeed. This kind of PK test, being technically much simpler, seemed as a reasonable beginning. Before going into specific experiments, however, let me present a different approach that leads to the same end.
Experiments with different types of "electronic coinflippers" as well as experiments with dice report PK effects of the same order of magnitude. In particular, nobody has been able to produce a random generator that is noticeably more sensitive to mental efforts than other generators.
For a systematic comparison of PK action on different random generators, one has to present the generators so that the subject and the experimenter cannot tell them apart, because we want the comparison made under psychologically identical conditions. Such studies (Schmidt, 1974) suggest (within the limited power of comparison tests mentioned earlier) that the nature of the random enerator does not affect the PK scores. (Psychological factors like the subject's motivation, the form of display, and the rate at which the random events are presented may make a great difference for the scores.)
This leads us, tentatively, to the following "Equivalence Hypothesis":
If we have two truly random binary generators, operating such that the generators are from the outside physically indistinguishable, then a PK effort affects the systems to the same degree, i.e., the systems are also undistinguishable in their response to a PK effort.
This hypothesis appears particularly appealing because, like the earlier hypothesis about the weak violation of physics, it is very simple and universal. And no matter whether or not these hypotheses will finally turn out to be quite correct, they can stimulate novel and provocative experiments.
Most participants in PK experiments use, subjectively, a goal oriented approach, focusing on the desired outcome like the lighting of a red lamp rather than on the internal operation of the random generator. The finding that the success rate is rather independent of the physical structure of the generator, furthermore, suggests that goal orientation may be a feature of the underlying mechanism rather than a matter of mere psychological attitude. It appears as if the subject, by concentrating on the final outcome, could induce nature to let the previous random events properly fall into place such as to lead to the desired outcome. This suggests an element of non-causality in the sense that the subject's present mental effort could affect the previous decisions of the random generator.
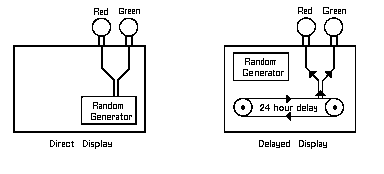
Fig. 2. PK effect on pre-recorded random events. Each of these "black boxes" displays two lamps, flashing in random sequence. For the physicist, the boxes are from the outside indistinguishable. The equivalence hypothesis requires that the two systems are also undistinguishable in their response to PK efforts
To study this explicitly, consider the two "black boxes" in Figure 2. The boxes contain similar internal random generators, producing continuous streams of binary decisions. The difference is that the left system displays these decisions immediately, whereas the right system displays each decision only after a 24-hour delay.
Both boxes with their continuously randomly flashing lights being physically undistinguishable from the outside, the equivalence hypothesis implies that a PK effort should affect the right box as well as the left one. This is, indeed, confirmed by the experiments to be discussed below. But success of a PK effort on the right box seems to violate our common concept of causality. We feel that the subject's effort at the time of the display, 24 hours after the random events, comes too late to be effective.
On the other hand, physicists have toyed occasionally with non-causal systems (Schmidt, 1966, 1981; Wheeler & Feynman, 1945) and shown that causality is not a logical necessity. Perhaps, physicists were just lucky in that most of this world can be described in terms of causal mechanisms so that the conceptual and mathematical complexities of non-causal systems could be avoided. And perhaps non-causality is the feature that makes psychic effects appear so intuitively implausible and "unphysical."
Let us look next at the experimental evidence that PK efforts can still succeed in a setting similar to the right side of Figure 2, where the random events are generated and recorded long before the subject makes a PK effort.
Consider the following test arrangement (Schmidt, 1976). A binary generator produces blocks of 201 random decisions. These are recorded simultaneously on two cassette tapes, with the heads and tails as signals in the right or left stereo channels respectively. At the generation speed of 20 signals per second, the tapes can hold typically 140 data blocks, with 20 second pauses between the blocks.
When the recording is completed, one of the identical tapes is placed into a safe, while the other tape is used in the PK sessions. During these sessions, the subject listens through headphones to the tape, perceiving the signals as clicks in the right or left ear. The subject's PK goal is an increased rate of clicks in the right ear, corresponding to an excess of generated heads. Whenever the subject gets tired, he can stop at any of the 20 second pauses on the tape and adjourn the test.
For the experiment, six tape pairs were pre-recorded in this manner, with a total of 832 blocks of 201 signals each. After the subject had worked on all tapes, the tapes were evaluated to see whether there was, indeed, a bias towards heads as aimed for by the subject. The simple but reliable evaluation method counted the number of successful blocks with more heads than tails and the number of unsuccessful blocks. The result showed that 54.6% of the 832 blocks were successful. This is statistically significant with odds against chance of 100:1.
A series of subsequent similar experiments (Schmidt 1976; Schmidt, Morris, & Rudolph, 1986) confirmed the PK effect with pre-recorded events, at high levels of statistical significance (z-value of 3.1, 4.2, 2.0, and 2.7).
To complete our discussion, remember that the initially generated random events were identically recorded on two cassette tapes, with one tape given to the subject and the other one kept locked in a safe. The correspondence of the two tape copies was guaranteed by a macroscopic recording process not subject to chance factors. According to our weak violation hypothesis, the PK effort should not alter the correspondence between the two records. This was, indeed, verified: the two records still agreed at the end, both showing the same bias towards heads.
Thus, the results suggest a non-local interaction in the sense that a PK effort on one tape is observable on the other tape also. This may remind us of the quantum correlations between far separated systems as discussed in connection with the Einstein-Podolsky-Rosen paradox. But there is the vital difference that the quantum correlation alone, no matter how puzzling and exotic it may appear, cannot be practically used for information transmission.
The exotic features of PK, on the other hand, can be made practically useful. As a side benefit, we can make PK testing particularly convenient and safe. We can let the subject work with the tape unsupervised at his home. We do not have to worry about the possibility of fraud, because we can evaluate the experiment from the tape in the safe, which never was near the subject.
We can carry this one step further and make the experiment safe even against errors and fraud by the experimenter, by channeling first hand evidence for psychic effects to an outsider, as follows.
First, we prepare a pair of tapes with identical sequences of random numbers. Next, we give one sealed tape copy to the outsider, letting the outsider decide whether he wants an excess of signals in the right or the left tape channel. We communicate this target assignment to the subject, who can now start the test sessions, playing the tape back while trying to get more signals in the specified channel. At the ends the outsider counts the numbers of right and left signals on his tape. And if the PK subject was successful, the outsider finds that, indeed, there are more signals in the channel he specified. If we repeat this procedure with a sufficient number of tapes, the outsider cannot but acknowledge the anomalous correlation between what he specified and what he later found on his tape.
We have used this basic method, with minor modifications, for an actual experiment, with myself as the experimenter and Bob Morris and Lu Rudolph at Syracuse University in the role of outsiders (Schmidt et al., 1986). Morris is an active parapsychology researcher and Rudolph a professor in communication engineering. Both felt rather skeptical with regard to PK effects on pre-recorded events. We used two outside observers supervising each other, because we also wanted to minimize the possibility of fraud by the outsiders.
The whole experiment was structured into ten sections, with each section to be evaluated by its z-value (the observed deviation in units of one standard deviation), positive values indicating success and negative values indicating failure. Figure 3 shows that only one of the ten sections gave a negative score.
The total result, as seen by the outsiders, is significant with odds against chance of 100:1 (z = 2.7).
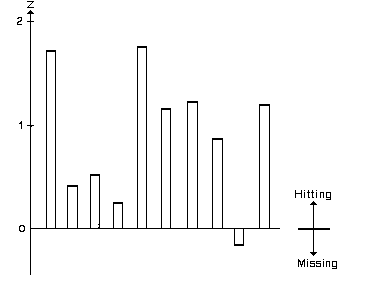
Fig. 3. Results of an experiment in channeling PK to outsiders. The figure plots the z-score obtained for the ten sections of the experiment. Positive values indicate scoring in the desired direction. Under the chance hypothesis, positive and negative z -values are equally likely.
Psychic phenomena being at odds with current physics as well as with naive intuition, we cannot explain the effects in terms of more familiar concepts. For the theorist, the ultimate "explanation" might consist of an abstract formalism that, like the formalisms of quantum theory or relativity theory, describes the observed phenomena consistently, teaching us to adjust our tuition accordingly. For the more practically inclined experimenter, "understanding" might be equivalent to sufficient hand's on experience and full information on what psychic mechanisms can and can not do.
The two hypothesis we have introduced might, if confirmed, serve as stepping stones for a future theory. The results of the experiments with pre-recorded random events were consistent with the hypotheses. But there are details that one might want to check more thoroughly.
The most basic question is whether it was really the subject in his time delayed PK effort that produced the effects. Let us consider some alternatives.
In view of the goal oriented operation of PK, the experimenter might have sensed the outsider's future target assignments and might have (unwittingly) activated his PK powers accordingly, at the time the random events were generated. While such a possibility cannot yet be ruled out completely, earlier experiments (Schmidt, 1976) in which subjects selected by their high success in regular PK experiment performed also particularly well in tests with pre-recorded PK targets point strongly to the subject as the PK source.
More information on this question of whether the subject's effort, indeed, is the source of the PK effect might come from experiments comparing the subject's mental state (during the PK session) with the resulting scores.
Another possibility to consider is that the outsider who generated the random target assignments could have been the source of the success. The outsider might have sensed the previously generated random numbers and influenced the generator for the random assignments accordingly. This argument would apply, however, only to the last experiment, because the earlier tests with pre-recorded targets did not involve such an outsider.
The weak violation hypothesis and the equivalence hypothesis agree in suggesting that PK tests with pre-recorded events should work as well as other PK tests. The weak violation hypothesis with its specific reference to quantum theory, however, introduces an additional element that we should discuss in some detail.
Quantum theory brought changes in our view of physical reality and the role of the observer in physics. These changes may be relevant for the interpretation of PK tests with pre-recorded events.
The reality problem appears most directly at the microscopic level. considering an electron or a photon, for example, we can measure the position of the particle, but we must not conclude that the particle always has a well specified position. Otherwise we get into conflict with the results of interference experiments. Thus, the location of a particle before a measurement does not have the kind of absolute physical reality that we customarily assign to the outside world. With quantum theory making no basic distinction between large and small systems, however, a reality question arises also for the macroscopic realm. This has been emphasized by recent experimental work related to Bell's theorem and the Einstein-Podolsky-Rosen paradox (d'Espagnat, 1976, 1979).
Consider, for example, the case where a decision from a binary random generator is recorded as a signal in the right or left channel of a cassette recorder. Then, prior to any observation of the outcome, quantum theory represents the state vector of the system as a superposition
of two macroscopically different physical states, where |R-STATE> corresponds to a situation with a "head" generated and signals recorded in the right channels of each tape, while |L-STATE> corresponds to the other possibility that a "tail" was generated and signals were recorded in the left channels of the two tapes.
Intuitively, we feel that nature, at this stage, must have decided on one or the other outcome. But the formalism of quantum theory contains no parameter which could tell us when such a decision is "really" made. Rather, the formalism suggests that the appearance of a head or a tail remains as unreal as the position of a particle until the outcome has been observed.
This leaves the question of the nature of the mechanism that transforms the |STATE> of the equation into either one of the macroscopically unambiguous states, |L-STATE> or |R-STATE>.
Conventional quantum theory answers this question very simply by interpreting the state vector not as a measure for some absolute physical reality but only as a measure of the observer's information about the system. Then the macroscopically ambiguous state of equation (1) reflects only the observers ignorance. And the sudden change of the observer's knowledge during a measurement is naturally accompanied by a sudden jump of the state vector (the collapse of the state vector) into the |L-STATE> or the |R-STATE>.
The mathematical elegance and logical consistency of quantum theory in this interpretation has suggested to many physicists that quantum theory has universal validity, giving the best possible description of nature, for small and large systems, and even for systems that include human subjects.
From the described experiments we can conclude, however, that such an universality claim must be wrong. Systems that contain a human subject can show features, like the discussed anomalous correlation between the subject's wish and an external random event, that are inconsistent with quantum theory.
Independent of the results of parapsychology, the early pioneers of quantum theory had already felt uneasy about this theory which admits reality only with regard to an observer, but does not explain if or in which respect the human observer is special (London & Bauer, 1939; von Neumann, 1932/1955; Wigner, 1962). This has led to many attempts at modifying or re-interpreting quantum theory. Let me mention only a few of these attempts, not because they should be taken particularly seriously, but because they might stimulate PK experimenters.
Eugene Wigner suggested that current quantum theory is not quite complete, that it lacks a specific description of the role of the experimenter. Wigner proposes that in the absence of an observer the state vector follows Schroedinger's equation, but that in the act of observation, some still unknown mechanism takes over, transforming the state of Eq. (1) into either the |R-STATE> or the |L-STATE> Thus, the collapse of the state vector assumes some physical reality of its own.
The active role played the observer in collapsing the state vector might provide an opening for PK effects to enter. This possibility and its experimental implications have been pursued by the author (Schmidt, 1981), and a specific model for the underlying mechanism, based on a hidden variable model by Bohm and Bub, has been studied by Mattuck and Walker (1979). Walker has also proposed several other interesting original ideas on the relationship between parapsychology and quantum theory. (Walker, 1979).
Wigner's model provides for minimal modifications quantum theory; only at the last stage where the observer (with his elusive element of consciousness) enters. In this model, there can still occur macroscopically ambiguous states like the one of the above equation, such as if physical reality before an observation could consist of two branches of reality, with nature still undecided.
As an alternative, one could consider modifications of quantum theory that provide for an automatic reduction of the state vector at some lower level, such that macroscopically ambiguous states could not arise. Such a model could still be consistent with all obtainable laboratory evidence, and, nevertheless, permit the concept of a macroscopically absolutely real world in which the observer is not basically different from other recording and computing equipment.
In our previous discussion of PK tests with pre-recorded events, we had implicitly assumed that macroscopic phenomena have an absolute reality, independent of any observation. From this viewpoint, nature made a final decision on the outcome of a random event, the event "really" happened, when the outcome was recorded on the cassette tapes. This led us to talk about causality violation in the sense that the subject's later mental effort affected the outcome of a previous random event.
Quantum theory, in the conventional form or in Wigner's version, however, permits a different interpretation: With the outcome of the random decision not observed before the PK session, nature had made no previous decision yet. The PK subject encountered a physical reality composed of two equally real potential branches. Therefore, the subject's PK effort did not have to reach into the past. Rather, the subject's observation transformed the still ambiguous reality into one of the macroscopically unique branches; and in this process of state vector collapse the subject also produced a PK effect, a slight change in the conventional transition probabilities.
From this viewpoint, the PK mechanism should no longer work if the outcome of the random decisions were observed by someone else before the subject made the PK effort. The previous observation should collapse the state vector, forcing nature into a final decision, so that there would be nothing left to change for the PK subject.
The only experiment in this direction done so far (Schmidt, 1985), indicates, indeed, such an inhibition of the PK effect by previous observation.
For this experiment, 80 sequences of 128 random bits were initially prerecorded. Each bit sequence could be displayed in a one minute test run by a pendulum swinging at a computer screen with slowly varying amplitude. (Basically a "1" in the bit sequence increased and a "0" decreased the amplitude of the next cycle).
At the start of each run, according to a fixed schedule, the subject was instructed either to aim for a high or a low pendulum amplitude. The resulting score measured the deviation (from chance expectancy) of the average amplitude in the specified direction.
Each sequence was displayed subsequently to two subjects, a test subject with a record of good PK performance, and a control subject with no demonstrable PK ability.
The sessions were timed such that in half of the runs the PK subject was the first to make the PK effort and in the other half the control subject. Furthermore, for each condition, the subjects aimed in half of the runs in the same and in the other half in opposite directions. The subjects were kept ignorant of these conditions.
Figure 4 shows that the PK test subject was successful only when being the first to see the random events in a run (Z = 3.1), whereas the previous observation by the control subject brought the score of the PK test subjects chose to chance (Z = -0.7). The control subject did not show a significant PK effect, even when acting as the first observer.
With only one experiment of this kind available, one might not want to draw a final conclusion but rather wait for future confirmations. And if, indeed, an initial human observation can block a subsequent PK effort, then we would want to know whether observation by a cat or even some lower animal might have the same effect. We might even be able to operationally define a "conscious observation" in terms of its effect on a subsequent PK effort.
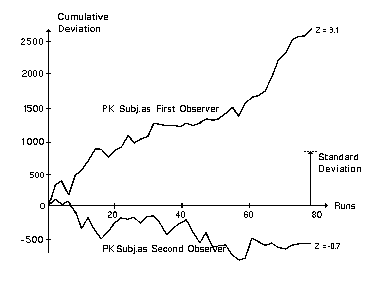
Fig. 4. Result of an experiment in which a PK subject (with a history of PK success) and a control subject (with no apparent PK ability) made consecutive PK efforts on the same pre-recorded events. In the half of the runs where the PK subject made the first effort his cumulative score (upper curve) reached a significant level. But in the other half of the runs, where the control subject had seen the outcome of the random events first, the PK subject's effort was no longer successful (lower curve).
Quantum theory has raised some still puzzling questions with regard to the role of the observer and the nature of reality. At the same time, the mathematical elegance and the logical consistency of quantum theory has suggested that the theory may have universal validity, being applicable even to systems that include human subjects. And with conventional quantum theory apparently experimentally correct, there seemed little demand for modifications with their inherent mathematical complications.
The results of parapsychology, on the other hand, indicate that quantum theory can be experimentally wrong when applied to systems that include a human subject. Experiments like the reported ones, point to specific links between the quantum formalism and psychic effects, suggesting a wealth of further interesting experiments. It remains to be seen whether the results will lead to a new quantum theory that includes psychic effects within its mathematical formalism, or whether they will merely outline some final limitation of the quantum formalism.
 RetroPsychoKinesis Project Home
RetroPsychoKinesis Project Home