
C-ship: The Dilation of Time


|
C-ship: The Dilation of Time |

|
Time in the moving system will be observed by a stationary observer to be running slower by the factor:
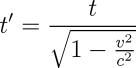
Which is the reciprocal of the equation for the Lorentz contraction. As with the Lorentz contraction, effects are negligible for small velocities, increase asymptotically as velocity approaches the speed of light.
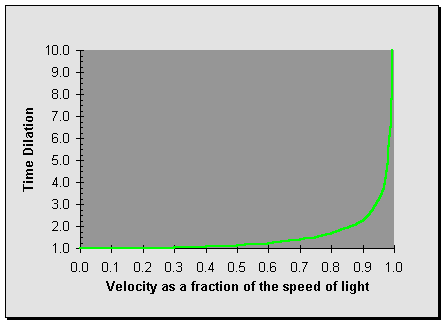
The following table illustrates how insignificant the effect of time dilation are for velocities as great as half the speed of light, but how dramatic it becomes as you draw ever closer to the speed of light. For each velocity, the time which elapses in the rest frame for each day measured by the ship's clock is given. By the time we reach 90% of the speed of light, for each day on board, two and a quarter days pass for an observer stationary with the respect to the Lattice. As we start tacking on nines to our velocity, time dilation becomes ever more extreme. At 0.999999 of the speed of light, almost two years pass in the Lattice for every ship's day. If we continue to accelerate to 0.99999999999999 c, for every day on board, nearly twenty thousand years pass for the observer at rest.
| Rest Frame Elapsed per Day on Ship |
||
|---|---|---|
| v/c | Days | Years |
| 0.0 | 1.00 | 0.003 |
| 0.1 | 1.01 | 0.003 |
| 0.2 | 1.02 | 0.003 |
| 0.3 | 1.05 | 0.003 |
| 0.4 | 1.09 | 0.003 |
| 0.5 | 1.15 | 0.003 |
| 0.6 | 1.25 | 0.003 |
| 0.7 | 1.40 | 0.004 |
| 0.8 | 1.67 | 0.005 |
| 0.9 | 2.29 | 0.006 |
| 0.95 | 3.20 | 0.009 |
| 0.97 | 4.11 | 0.011 |
| 0.99 | 7.09 | 0.019 |
| 0.995 | 10.01 | 0.027 |
| 0.999 | 22.37 | 0.061 |
| 0.9999 | 70.71 | 0.194 |
| 0.99999 | 223.61 | 0.613 |
| 0.999999 | 707.11 | 1.937 |
| 0.9999999 | 2236.07 | 6.126 |
| 0.99999999 | 7071.07 | 19.373 |
| 0.999999999 | 22360.68 | 61.262 |
| 0.9999999999 | 70710.68 | 193.728 |
| 0.99999999999 | 223606.79 | 612.621 |
| 0.999999999999 | 707114.60 | 1937.300 |
| 0.9999999999999 | 2235720.41 | 6125.261 |
| 0.99999999999999 | 7073895.38 | 19380.535 |
| 0.999999999999999 | 22369621.33 | 61286.634 |
At the velocities people currently travel the effect of time dilation is small, but measurable with accurate instruments. Since time dilation affects the rate at which time passes, the total discrepancy between stationary and moving clocks increases throughout the voyage. Several Russian cosmonauts have spent a year or more in Earth orbit on the space station Mir. Their orbital velocity, about 7700 metres per second, is only 0.0000257 times the speed of light, yielding a time dilation factor of 1.00000000033; each second on board Mir, 1.00000000033 seconds pass on Earth. For every second you age on Earth, the cosmonaut in orbit ages 3 nanoseconds less. This doesn't seem like much, but it adds up; after a year the cosmonaut's watch will be 3.8 seconds behind your earthbound timepiece.
You don't even have to go into orbit to measure time dilation. Modern-day atomic clocks are so accurate that when synchronising clocks between different observatories, the effect of time dilation due to transporting the reference clock on an airline flight must be taken into account.
You'll see dilation of time in action when we embark on a mission to fly through the Lattice. As you step through the movie frame by frame, compare the ship's clock with the clock at rest with regard to the Lattice, noting how the discrepancy increases as the ship's velocity approaches the speed of light.