C-ship: The Doppler Shift

In 1842, the Austrian physicist Christian Johann Doppler noted that the wavelength of light, sound, or any other kind of propagating energy measured by a moving observer will be shifted by a factor of:

where v is the velocity at which the observer is approaching or receding from the source and c is the speed at which the wave propagates.

We're all familiar with the Doppler shift of sound waves. If we stand by the tracks and listen to a train pass, the sound of its horn will be shifted to higher pitch as the train approaches, then abruptly to lower pitch as it passes by us and recedes.

Sound travels about 350 metres per second. A train travelling at 120 kilometres per hour is moving 33⅓ metres per second, or roughly one tenth the speed of sound. From Doppler's formula, we can expect the frequency of sound approaching the train to be shifted to 10% higher pitch, and sounds receding shifted to 10% lower pitch, roughly the difference between two adjacent white keys on a piano keyboard. If a pipe organ in a church near the train tracks is playing this note, a passenger on a (very quiet Swiss) train approaching the church at 120 km/hour will hear the note shifted upward by about 10% in frequency. After the train passes the church, the note will be heard shifted down by the same percentage. Here's the three notes played together so you can hear the difference more clearly.

The reason we notice the Doppler shift of sound but not of light is simply the consequence of the tremendous difference in the speed of sound and the speed of light. There's an apocryphal story about the physicist who tried to beat a ticket for running a red light by telling the judge that at the speed he was approaching the signal, the red light was Doppler shifted so it appeared green. The judge pondered this for a few minutes and tore up the red light ticket. Then, seeing as the physicist would have to be driving about a quarter of the speed of light to see a red signal as green, the judge fined him 269 million dollars for speeding, one dollar for each kilometer per hour over the limit.

To correctly calculate the Doppler shift for large velocities, we have to take into account the Lorentz contraction of spacetime. As we travel along the propagating wave, the rate at which we encounter peaks and troughs is affected not only by the ratio of our velocity to the speed the wave is travelling, but also by the Lorentz contraction in the direction of our travel.

When we're approaching a wave, Lorentz contraction increases the Doppler shift we observe since the wave crests become increasingly contracted in space; consequently we measure a shorter wavelength. Since the Lorentz contraction increases without bound as we approach the speed of light, so the Doppler shift increases without bound, rather than merely doubling the frequency as we'd expect from classical physics.

If we're receding from the wave, the Doppler shift is reduced by special relativity. Why? The Lorentz contraction is the same regardless of whether we're approaching an object or receding from it. The Lorentz contraction will, then, reduce the wavelength of the wave at the same time the Doppler shift is increasing it.

The Doppler shift of plane light waves in vacuum which arrive with an angle ϕ with respect to the direction of travel is:

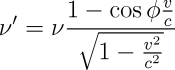
The difference in the classical and relativistic Doppler effects can be seen in the following graph showing the wavelength shift of green light for velocities ranging from v/c=−1 (recession at the speed of light) to v/c=1 (approach at the speed of light). The Doppler shift predicted by classical physics is shown in red and the correct prediction of special relativity in green.

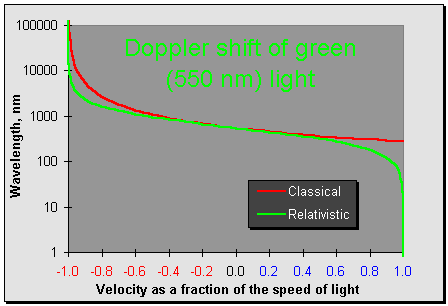
The overlapping of the two curves in the middle of the graph, where velocities are relatively small compared to the speed of light, demonstrates how relativistic effects have little impact at velocities below a substantial fraction of the speed of light. Note how the interaction of the classical Doppler shift and Lorentz contraction affects the two ends of the graph in different ways. For extreme approach velocities, relativity predicts a blue shift diverging toward infinity while the classical equation only halves the wavelength at rest. For large velocities of recession, both classical and relativistic equations show the wavelength approaching infinitely long values; here the Lorentz contraction reduces the amount of the Doppler shift while leaving intact the trend toward infinite wavelength.

Onward to The Aberration of Light

Backward to The Dilation of Time

Up to C-ship