
C-ship: The Aberration of Light


|
C-ship: The Aberration of Light |

|
Unlike the Lorentz contraction or the dilation of time, which are purely relativistic effects with no counterparts in classical (Newtonian) physics, the aberration of light is predicted by classical physics and was first demonstrated in 1725, two years before Newton's death. Special relativity modifies the classical formula for aberration, predicting results which differ substantially from those of classical physics only for objects moving at a substantial fraction of the speed of light.
To understand relativistic aberration, we'll start by exploring classical aberration to better understand the changes required by special relativity. Before we set out in our C-ship to explore the aberration of light, let's warm up by taking a journey in a much more familiar environment, a European train crossing the countryside during a typical European drizzle.
We start out sitting in our seats in the station, having just boarded the train, looking at the rain as it falls straight down from the sky. We're stationary, and the raindrops are falling at 60 kilometres per hour, their terminal velocity in the air.
 0 km/hour
0 km/hour
Now the train pulls out of the station and begins to accelerate. As it reaches 30 kilometers per hour, the view out the window looks like:
 30 km/hour
30 km/hour
Even though the rain is still falling straight down, it appears to be falling toward the train. The reason is obvious if you think about; as each raindrop falls, we're moving toward it, so we observe it to follow a slanted path, with the slant increasing as we travel faster compared to the speed at which the drop is falling. As the train reaches 60 kilometers per hour, it's travelling as rapidly to the left, as seen from our window, as the rain is falling from the sky. As a result, we see the rain streaming toward us at an apparent angle of 45°—the downward motion due to the rain's falling, the equal sideways motion the result of the train's velocity with respect to the raindrops.
 60 km/hour
60 km/hour
By the time the train reaches its cruising speed of 250 km/hour (we're on board the French Train à Grande Vitesse, bien sûr) our horizontal velocity is more than four times the speed at which the raindrops are falling, so they appear to be travelling almost horizontally when we look from the side of the train.
 250 km/hour
250 km/hour
Now consider how this looks from the standpoint of the engineer sitting in the cab at the front of the train. In the station, the drops fall straight down. But as the train goes faster and faster, they approach the windshield at angles closer and closer to the horizontal as the speed increases.
Raindrops keep fallin' in my face,
More and more as I pick up the pace…
To illustrate this a little more clearly, consider a unlucky soul riding a bicycle in the downpour our train is rushing through. The rider has a hat with a small bill, and as long as he's stopped the rain, which is falling vertically, doesn't get in his face. But the faster he rides, the more horizontal the oncoming rain becomes, and soon his hat is useless, since the rain approaches at an angle which strikes his face directly.
In classical physics, the aberration of light is precisely like the aberration of rain we've just experienced; the only difference is that light travels considerably faster than rain, about 18 million times faster, as a matter of fact. The aberration observed depends only on the speed of the object and the speed you're travelling with respect to it. Photons of light emitted vertically toward the ground by trackside lights will slant just like the raindrops due to the train's motion, but with an angle eighteen million times smaller. No wonder you don't notice.
But that doesn't mean aberration of light can't be seen from the Earth. By the early eighteenth century the idea that the Earth revolved around the Sun, first propounded by Nicholas Copernicus in the mid-sixteenth century, was accepted by most learned people. And yet, as late as 1725, there was no direct proof that the Earth moved with regard to the distant stars and was not, therefore, at the centre of the universe.
One way to prove the Earth moved would be to measure the parallax of a star. When you move your head from side to side, objects close to you seem to shift their position with respect to those more distant. If the Earth truly traced out an orbit with a diameter of almost 300 million kilometers every year, then shouldn't nearby stars seem to shift their position with regard to distant stars when observed six months apart (when the Earth is on opposite sides of its orbit around the Sun)?
Yet, in the time of Copernicus and for almost three centuries thereafter, no star had been observed to exhibit the effect of parallax. This was cited by diehard geocentrists as proof that the Earth did not really move. Copernicus and his followers argued (correctly) that no parallax had been seen because the stars were so distant that even with a baseline of 300 million kilometers, the apparent motion of even the nearest stars was too small for existing telescopes to detect. Compounding the problem was that fact that until the parallax of a star was measured, astronomers had no idea of the distance to any star, and therefore no clue to the distance scale of the universe beyond the solar system.
In 1725 James Bradley, an English amateur astronomer, was attempting to observe stellar parallax when, through meticulous observation he observed that stars did trace out small ellipses in the sky as expected for parallax, but that all stars traced out precisely the same ellipses! This didn't make any sense at all; the only way the parallax of all stars could be same would be if all the stars were the same distance from the Earth—a regression to the Earth-centred universe with a vengeance! After a while, the apparent motion Bradley observed was discovered to be the result of the aberration of light. On each point in its orbit, the Earth is travelling with a velocity with respect to the distant stars that differs by 60 kilometers per second from the velocity at the opposing point—where the Earth will be six months hence.
Now 60 kilometers a second is pretty fast compared to freeway speed limits or even the velocity of Earth satellites, but it's only 0.02% of the speed of light. However, by Bradley's time the art and science of measuring the positions of stars had advanced to such an extent that he was able to observe the mere 41 arc-second displacement of the apparent position of stars due to aberration.
It wasn't until 1837 that astronomers managed to measure the much smaller parallax of the nearest stars. The classical aberration of light discovered by Bradley must be taken into account whenever accurate positions of objects in the sky are calculated.
In classical physics, the aberration of light works just like the aberration of rain—it depends on the ratio of the speed you're going to the speed of light. It's only because the speed of light is so great that it takes precise measurement of the position of stars to make aberration apparent. Classical physics, then, predicts that if we were to travel at the speed of light we'd measure the aberration of light from a source orthogonal to our direction of travel to be 45°.
But that implies we could continue to accelerate past the speed of light and measure greater and greater angles of aberration, just as the TGV does when it exceeds the speed at which the rain is falling. Not possible—in special relativity no material object can attain the speed of light. When the Lorentz transform is applied to the aberration of light, we discover that the the aberration measured by an observer travelling at velocity v for light from a distant source at direction ϕ in the rest frame is:
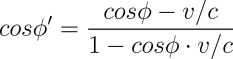
As we've become accustomed to in discussing other relativistic effects, the aberration predicted by this equation agrees closely with that predicted by classical physics for velocities much less than that of light. It's only as you approach the speed of light that special relativistic effects become manifest. The table below shows the aberration predicted by classical physics and by special relativity for various velocities. For small velocities the differences are small, but as you approach the speed of light, where classical physics predicts an aberration of 45°, special relativity shows the aberration to increase without bound, so that light rays arriving from any direction other than directly opposite to the direction of motion are seen to approach a point directly in front of the moving observer.
| Velocity v/c |
Classical Prediction ° |
Relativistic Aberration ° | Discrepancy: Classical − Relativity |
|---|---|---|---|
| 0.0 | 90.000000 | 90.000000 | 0.000000 |
| 0.1 | 84.289407 | 84.260830 | 0.028577 |
| 0.2 | 78.690068 | 78.463041 | 0.227027 |
| 0.3 | 73.300756 | 72.542397 | 0.758359 |
| 0.4 | 68.198591 | 66.421822 | 1.776769 |
| 0.5 | 63.434949 | 60.000000 | 3.434949 |
| 0.6 | 59.036243 | 53.130102 | 5.906141 |
| 0.7 | 55.007980 | 45.572996 | 9.434984 |
| 0.8 | 51.340192 | 36.869898 | 14.470294 |
| 0.9 | 48.012788 | 25.841933 | 22.170855 |
| 0.95 | 46.468801 | 18.194872 | 28.273928 |
| 0.97 | 45.872457 | 14.069868 | 31.802589 |
| 0.99 | 45.287916 | 8.109614 | 37.178302 |
| 0.995 | 45.143598 | 5.731968 | 39.411630 |
| 0.999 | 45.028662 | 2.562559 | 42.466103 |
| 0.9999 | 45.002865 | 0.810291 | 44.192573 |
| 0.99999 | 45.000286 | 0.256235 | 44.744052 |
| 0.999999 | 45.000029 | 0.081028 | 44.919000 |
| 0.9999999 | 45.000003 | 0.025623 | 44.974379 |
| 0.99999999 | 45.000000 | 0.008103 | 44.991897 |
| 0.999999999 | 45.000000 | 0.002562 | 44.997438 |
| 0.9999999999 | 45.000000 | 0.000810 | 44.999190 |
| 0.99999999999 | 45.000000 | 0.000256 | 44.999744 |
| 0.999999999999 | 45.000000 | 0.000081 | 44.999919 |
| 0.9999999999999 | 45.000000 | 0.000026 | 44.999974 |
| 0.99999999999999 | 45.000000 | 0.000008 | 44.999992 |
| 0.999999999999999 | 45.000000 | 0.000002 | 44.999998 |
Let's board C-ship Bradley to explore relativistic aberration. To avoid being confused by other relativistic effects, we've set the main viewer to compensate for Lorentz contraction and Doppler shift, leaving only aberration to affect our view. Once again, we fly through the Lattice, this time arranging our flight profile so as to reach different velocities as we fly through the midpoint of the Lattice. The following animation shows the effects of aberration as the Bradley accelerates from rest with respect to the Lattice to near the speed of light.
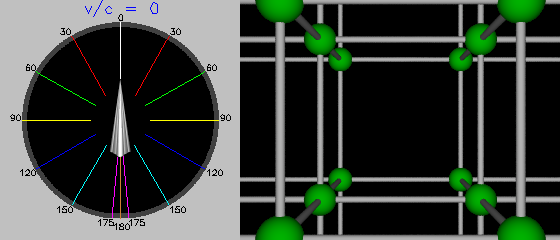
Now let's look at the frames of the movie in more detail. At rest in the middle of the Lattice, we see a normal view, unaffected by aberration. The ship's computer displays a graphic to the left of the viewscreen that shows the effect of aberration on light arriving from various directions with respect to the direction we're travelling. Stationary in the Lattice, no aberration is indicated.
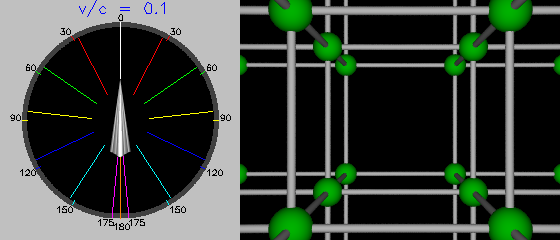
Now we've accelerated to one tenth the speed of light, and already aberration is changing our view. The display on the left shows how light from various directions (shown on the outer ring) has been displaced to the apparent directions of the lines radiating from the Bradley. At this velocity aberration agrees with the classical prediction to two decimal places; light is still behaving just like rain. We notice on the main viewer that we're seeing more of the lattice, as aberration shifts objects previously outside our field of view into the frame.
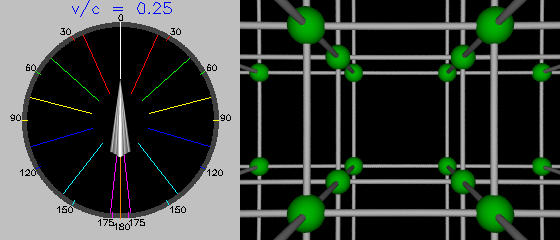
At a quarter of the speed of light, Newton is still firmly in charge; aberration is behaving linearly, and the contribution of special relativity is less than a quarter of a degree of the total aberration of more than 11°.
Half the speed of light, and we're developing eyes in the back of our head—objects 120° from the direction we're moving are shifted so they appear to our right and left. Still, relativity accounts for only about 10% of the total aberration.
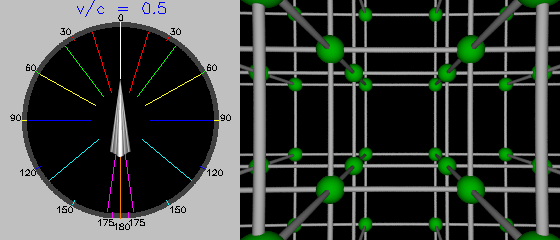
Three quarters of the speed of light: relativity now accounts for a substantial fraction of the total aberration, which is already approaching the 45° classical physics predicts we'd measure at the speed of light.
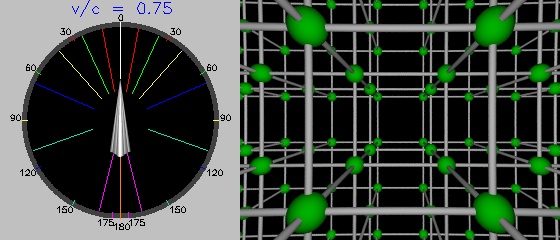
Nine-tenths of the speed of light: Einstein's in the driver's seat now. Light rays coming from our side now appear to come from a direction about 26° from the ship's bow, compared to the classical prediction of 48°. More and more of the Lattice seems to be before us now, even though we're observing from a point in the middle.
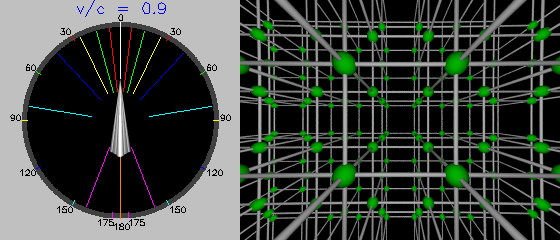
Ninety-five percent of the speed of light: the compression toward our direction of travel continues. Relativistic effects now dominate.
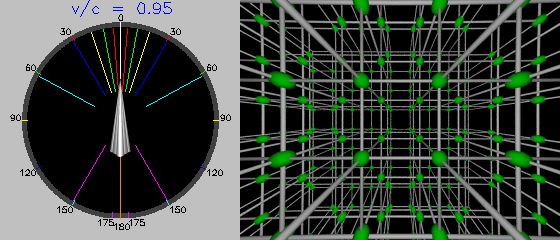
Ninety-nine percent: only objects almost directly astern still appear to be behind us.
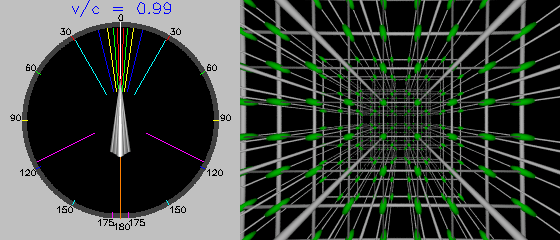
We're now only one part in a thousand slower than light. Even objects five degrees from our stern now enter the field of view looking in the direction of travel. Extreme distortion of objects behind us becomes apparent.
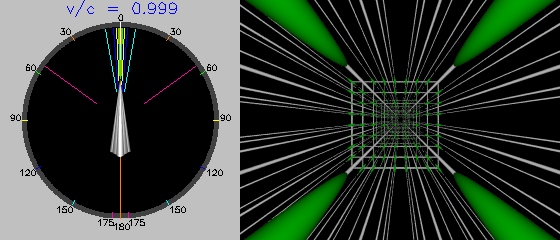
And finally, we view the Lattice from the midpoint at a velocity of 0.9999 of the speed of light. The cell of the Lattice directly behind our ship has been distorted by aberration to almost fill the field of view. The rest of the Lattice is reduced to a small grid in the centre of the main viewer. The readout to the left of the view shows that even light rays emitted five degrees from our stern appear at an angle to the bow of 15°.
