RetroPsychoKinesis Experiment Summary
Last updated: Friday 2012 February 3 5:02 UTC
This report is updated daily
Overall Summary
| Total experiments: | 345063 |
| Number of subjects: | 32285 |
| Total tries: | 353344512 |
| Total hits: | 176673480 |
| Overall z: | 0.1302 | standard deviations |
"Subjects" is the number of different E-mail addresses or "handles"
in the log file; there is no assurance a given individual may not
have entered a number of different identities, either intentionally
or by accident. The number of experiments includes only "for the
record" experiments, not those designated in advance by the subject
as "practice". Since each experiment involves 1024 bits, the
total number of "Tries" in the next line is
345063×1024, or 353344512. Examination of the logged
bit sequences sent to the subjects shows that 176673480 of the
total of 353344512 bits were "Hits"--they agree with the subject's
previously-chosen goal. There were, then, 1224 more bits among a
total of 353344512 consistent with the subjects' intent to bias the
generator. This is equivalent to changing one bit in every 288680 in
the direction desired by the subject. The measured bias amounts to
0.1302 standard deviations.
Hit Histogram
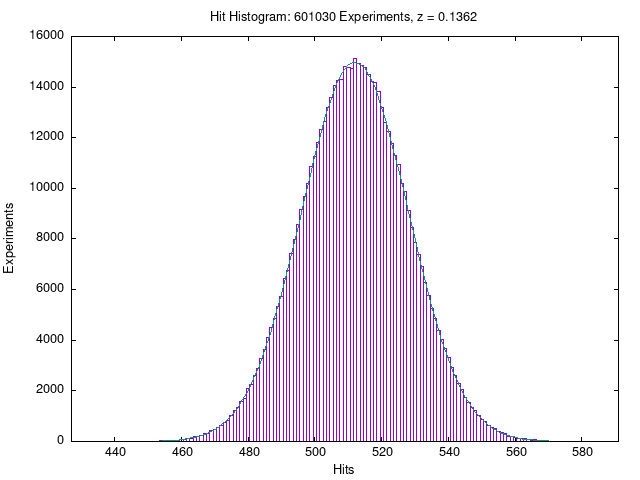
The following chart summarises the results of all for-the-record
experiments (excluding runs designated in advance as "practice"
runs by the subject, which are logged for completeness, but do not
figure in the statistical analysis) performed since the RPKP
experiments were begun in January of 1997.
The blue curve gives the
normal distribution for a large number of trials of 1024 events with
probability 0.5. (For a number of trials as large as 1024, the
binomial and normal distributions are equal on the scale of this
plot.) The red boxes show the actual number of experimental runs which
resulted in the given number of hits. A "hit" is defined as the
number of bits in the 1024 bit stream which agreed with the subject's
previously chosen one-or-zero goal.
Cumulative Deviation from Expectation
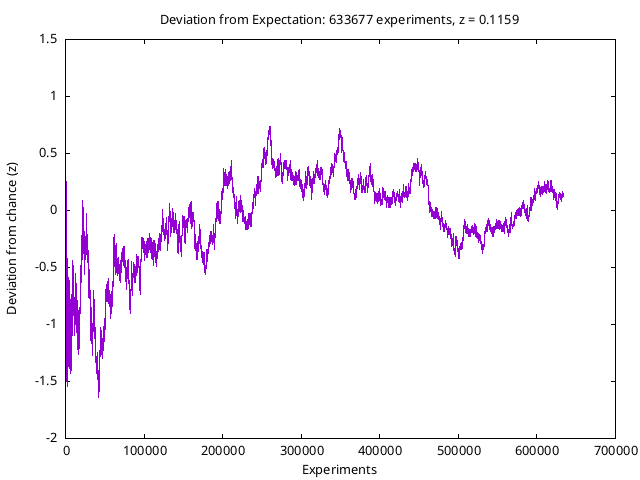
Any experiment involving a random data source can be
expected to, in the absence of perturbing influences,
follow a random walk around the most probable
value. As the number of experiments increases, overall
divergences should decrease.
When examining the results of
such experiments, it's important to satisfy
yourself that any non-chance effect you observe doesn't
result from the experimenter choosing to show you
results at a peak or trough of a series which is
swinging to both sides of the chance expectation
with a mean value equal to chance. The following is a
deviation plot of the all 345063 RPKP experiments
to date; it shows the absolute divergence of the experimental
results in the direction of bias preselected by the
subject compared to that expected by chance, and the
divergence in terms of standard deviations for the cumulative number
of trials for a probability of 0.5
on each trial.
Cumulative Deviation by Intent from Expectation
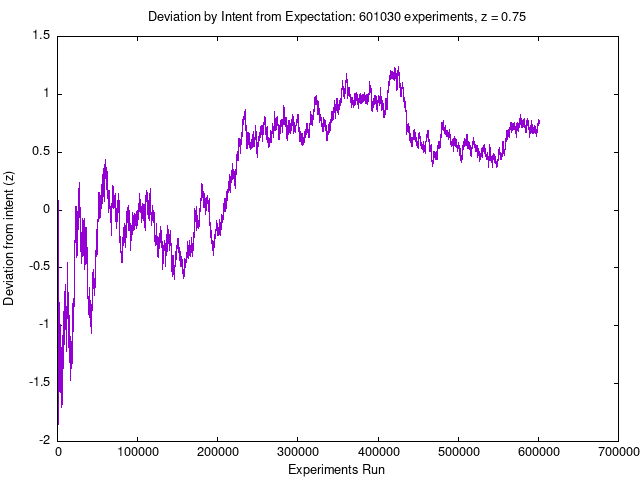
Another way to evaluate the results of the experiments is to
examine how frequently the result of an experiment (excess of
one or zero bits) agrees with the subject's pre-declared goal,
regardless of the magnitude of the deviation from the mean
value. If the subject has chosen a goal corresponding to an
excess of one bits, the experiment will be scored as a success
if there is any excess of one bits at all (513 one bits out of 1024
is just as much a success as 527 one bits and, conversely, 511
one bits is as much a failure as a result of 497 one bits).
If the subject chooses a goal corresponding to an excess of zero
bits, the sense of the comparison is inverted: any excess of
zero bits is deemed a success. To preserve symmetry, results with an
equal number of zero and one bits (512 each in an experiment
of 1024 bits) are considered neutral and do not change the
cumulative result. Here we plot the cumulative deviation
by intent as
z: the number of standard deviations by
which it differs from the expectation value of zero.
Runs by Subjects Histogram
The following table shows the number of experiments run by
various subjects, and the cumulative results and
standard deviation for each number of experiments.
Individual subjects who have made a large number of runs
appear show up at the bottom of the the table, and the
results they obtained can be compared.
Experiments
Run | Number of
Subjects | Hits/Tries | z |
|---|
| 1 | 12427 |
6354353/12725248 |
4.6372 |
| 2 | 5599 |
5729889/11466752 |
2.0595 |
| 3 | 3532 |
5422832/10850304 |
1.4086 |
| 4 | 2118 |
4334670/8675328 |
2.0330 |
| 5 | 1498 |
3836225/7669760 |
0.9713 |
| 6 | 1051 |
3229912/6457344 |
0.9759 |
| 7 | 757 |
2711122/5426176 |
1.6880 |
| 8 | 580 |
2376138/4751360 |
0.4202 |
| 9 | 503 |
2317438/4635648 |
0.3586 |
| 10 | 440 |
2252051/4505600 |
0.7057 |
| 11 | 337 |
1897930/3795968 |
0.0554 |
| 12 | 286 |
1757149/3514368 |
0.0373 |
| 13 | 258 |
1717098/3434496 |
0.1619 |
| 14 | 216 |
1548169/3096576 |
0.1352 |
| 15 | 205 |
1573875/3148800 |
0.5917 |
| 16 | 159 |
1303573/2605056 |
1.2949 |
| 17 | 130 |
1131939/2263040 |
0.5571 |
| 18 | 121 |
1115169/2230272 |
0.0442 |
| 19 | 115 |
1118532/2237440 |
0.2514 |
| 20 | 112 |
1147817/2293760 |
1.2374 |
| 21 | 93 |
999991/1999872 |
0.0778 |
| 22 | 82 |
923357/1847296 |
0.4282 |
| 23 | 68 |
800547/1601536 |
0.3493 |
| 24 | 60 |
737889/1474560 |
1.0030 |
| 25 | 69 |
883119/1766400 |
0.1219 |
| 26 | 58 |
773034/1544192 |
1.5097 |
| 27 | 59 |
815985/1631232 |
0.5778 |
| 28 | 44 |
631383/1261568 |
1.0666 |
| 29 | 47 |
696547/1395712 |
2.2160 |
| 30 | 50 |
766950/1536000 |
1.6944 |
| 31 | 40 |
635631/1269760 |
1.3329 |
| 32 | 48 |
787400/1572864 |
1.5437 |
| 33 | 42 |
710884/1419264 |
2.1019 |
| 34 | 34 |
591697/1183744 |
0.3217 |
| 35 | 25 |
448550/896000 |
1.1621 |
| 36 | 39 |
719969/1437696 |
1.8698 |
| 37 | 31 |
585759/1174528 |
2.7774 |
| 38 | 38 |
738888/1478656 |
0.7237 |
| 39 | 22 |
439019/878592 |
0.5910 |
| 40 | 33 |
676314/1351680 |
0.8154 |
| 41 | 25 |
525022/1049600 |
0.4334 |
| 42 | 21 |
451530/903168 |
0.1136 |
| 43 | 20 |
440298/880640 |
0.0469 |
| 44 | 21 |
473436/946176 |
0.7155 |
| 45 | 15 |
345310/691200 |
0.6976 |
| 46 | 18 |
423771/847872 |
0.3584 |
| 47 | 18 |
433353/866304 |
0.4319 |
| 48 | 14 |
343993/688128 |
0.1712 |
| 49 | 13 |
326191/652288 |
0.1164 |
| 50 | 16 |
409754/819200 |
0.3403 |
| 51 | 20 |
521715/1044480 |
1.0274 |
| 52 | 18 |
480134/958464 |
1.8427 |
| 53 | 12 |
325758/651264 |
0.3123 |
| 54 | 8 |
221293/442368 |
0.3278 |
| 55 | 16 |
451385/901120 |
1.7382 |
| 56 | 14 |
401931/802816 |
1.1674 |
| 57 | 9 |
262949/525312 |
0.8085 |
| 58 | 11 |
326542/653312 |
0.2821 |
| 59 | 10 |
302080/604160 |
0.0000 |
| 60 | 14 |
430130/860160 |
0.1078 |
| 61 | 10 |
312473/624640 |
0.3872 |
| 62 | 12 |
380828/761856 |
0.2291 |
| 63 | 13 |
419576/838656 |
0.5416 |
| 64 | 9 |
294357/589824 |
1.4453 |
| 65 | 6 |
199888/399360 |
0.6583 |
| 66 | 8 |
270253/540672 |
0.2258 |
| 67 | 10 |
343014/686080 |
0.0628 |
| 68 | 7 |
243870/487424 |
0.4526 |
| 69 | 6 |
212266/423936 |
0.9154 |
| 70 | 9 |
322748/645120 |
0.4681 |
| 71 | 8 |
290993/581632 |
0.4642 |
| 72 | 8 |
295314/589824 |
1.0469 |
| 73 | 4 |
149532/299008 |
0.1024 |
| 74 | 8 |
302371/606208 |
1.8829 |
| 75 | 7 |
268672/537600 |
0.3491 |
| 76 | 7 |
272289/544768 |
0.2574 |
| 77 | 4 |
157606/315392 |
0.3205 |
| 78 | 6 |
239761/479232 |
0.4189 |
| 79 | 4 |
162332/323584 |
1.8986 |
| 80 | 4 |
163989/327680 |
0.5206 |
| 81 | 4 |
165793/331776 |
0.3299 |
| 82 | 5 |
209804/419840 |
0.3581 |
| 83 | 1 |
42549/84992 |
0.3636 |
| 84 | 2 |
86078/172032 |
0.2990 |
| 85 | 3 |
130400/261120 |
0.6262 |
| 86 | 3 |
132049/264192 |
0.1829 |
| 87 | 2 |
88863/178176 |
1.0661 |
| 88 | 6 |
270223/540672 |
0.3074 |
| 89 | 1 |
45777/91136 |
1.3846 |
| 90 | 2 |
91843/184320 |
1.4767 |
| 91 | 3 |
139795/279552 |
0.0719 |
| 92 | 6 |
282565/565248 |
0.1570 |
| 93 | 4 |
190810/380928 |
1.1212 |
| 94 | 1 |
48134/96256 |
0.0387 |
| 95 | 5 |
242841/486400 |
1.0295 |
| 96 | 2 |
98517/196608 |
0.9607 |
| 97 | 5 |
248401/496640 |
0.2299 |
| 98 | 2 |
100457/200704 |
0.4688 |
| 99 | 5 |
253044/506880 |
1.1124 |
| 100 | 8 |
409549/819200 |
0.1127 |
| 101 | 6 |
310369/620544 |
0.2463 |
| 102 | 3 |
157014/313344 |
1.2219 |
| 103 | 3 |
158142/316416 |
0.2347 |
| 104 | 4 |
212797/425984 |
0.5975 |
| 106 | 2 |
108403/217088 |
0.6052 |
| 108 | 6 |
332151/663552 |
0.9207 |
| 109 | 1 |
55742/111616 |
0.3951 |
| 110 | 2 |
112340/225280 |
1.2641 |
| 111 | 4 |
227235/454656 |
0.2758 |
| 112 | 3 |
172072/344064 |
0.1364 |
| 113 | 2 |
115537/231424 |
0.7276 |
| 114 | 6 |
350617/700416 |
0.9774 |
| 115 | 5 |
295078/588800 |
1.7672 |
| 116 | 7 |
415998/831488 |
0.5571 |
| 117 | 1 |
59967/119808 |
0.3640 |
| 118 | 3 |
181086/362496 |
0.5381 |
| 119 | 3 |
183021/365568 |
0.7840 |
| 120 | 5 |
307260/614400 |
0.1531 |
| 121 | 1 |
62175/123904 |
1.2670 |
| 122 | 5 |
312322/624640 |
0.0051 |
| 123 | 2 |
125473/251904 |
1.9087 |
| 124 | 1 |
63580/126976 |
0.5164 |
| 126 | 2 |
128874/258048 |
0.5906 |
| 127 | 1 |
64968/130048 |
0.3106 |
| 128 | 1 |
65799/131072 |
1.4529 |
| 129 | 3 |
198940/396288 |
2.5289 |
| 130 | 4 |
266297/532480 |
0.1562 |
| 132 | 3 |
202354/405504 |
1.2500 |
| 133 | 1 |
67967/136192 |
0.6991 |
| 134 | 2 |
137337/274432 |
0.4620 |
| 135 | 3 |
207396/414720 |
0.1118 |
| 136 | 2 |
139092/278528 |
0.6518 |
| 137 | 1 |
69880/140288 |
1.4097 |
| 138 | 1 |
70624/141312 |
0.1703 |
| 139 | 1 |
71128/142336 |
0.2120 |
| 140 | 5 |
358635/716800 |
0.5551 |
| 141 | 2 |
144591/288768 |
0.7704 |
| 142 | 1 |
72469/145408 |
1.2325 |
| 143 | 2 |
146331/292864 |
0.3733 |
| 144 | 3 |
221358/442368 |
0.5232 |
| 145 | 3 |
222983/445440 |
0.7881 |
| 146 | 3 |
224483/448512 |
0.6779 |
| 148 | 2 |
151121/303104 |
1.5657 |
| 149 | 3 |
228586/457728 |
0.8218 |
| 150 | 5 |
384090/768000 |
0.2054 |
| 151 | 2 |
154761/309248 |
0.4927 |
| 153 | 3 |
235330/470016 |
0.9394 |
| 154 | 2 |
157861/315392 |
0.5876 |
| 155 | 1 |
79604/158720 |
1.2249 |
| 157 | 1 |
80384/160768 |
0.0000 |
| 158 | 1 |
80734/161792 |
0.8055 |
| 159 | 3 |
244373/488448 |
0.4264 |
| 160 | 1 |
82202/163840 |
1.3934 |
| 161 | 3 |
247386/494592 |
0.2559 |
| 162 | 3 |
249025/497664 |
0.5472 |
| 163 | 1 |
83338/166912 |
0.5777 |
| 164 | 1 |
83799/167936 |
0.8248 |
| 165 | 3 |
252908/506880 |
1.4945 |
| 166 | 1 |
85200/169984 |
1.0090 |
| 170 | 1 |
86917/174080 |
0.5896 |
| 171 | 2 |
174975/350208 |
0.4360 |
| 172 | 2 |
175786/352256 |
1.1525 |
| 173 | 1 |
88669/177152 |
0.4419 |
| 174 | 2 |
178518/356352 |
1.1458 |
| 175 | 3 |
268489/537600 |
0.8483 |
| 176 | 3 |
270562/540672 |
0.6147 |
| 177 | 1 |
90903/181248 |
1.3107 |
| 178 | 1 |
91056/182272 |
0.3748 |
| 180 | 2 |
184287/368640 |
0.1087 |
| 182 | 1 |
93122/186368 |
0.2872 |
| 183 | 1 |
93828/187392 |
0.6099 |
| 189 | 4 |
386880/774144 |
0.4364 |
| 191 | 1 |
97737/195584 |
0.2487 |
| 192 | 2 |
196641/393216 |
0.1053 |
| 195 | 1 |
99196/199680 |
2.8824 |
| 197 | 2 |
201707/403456 |
0.0661 |
| 200 | 1 |
102391/204800 |
0.0398 |
| 201 | 2 |
205561/411648 |
0.8198 |
| 202 | 1 |
103444/206848 |
0.0879 |
| 203 | 1 |
103788/207872 |
0.6492 |
| 204 | 2 |
209659/417792 |
2.3609 |
| 205 | 2 |
209993/419840 |
0.2253 |
| 208 | 1 |
106929/212992 |
1.8764 |
| 210 | 2 |
215776/430080 |
2.2446 |
| 212 | 2 |
217415/434176 |
0.9925 |
| 217 | 1 |
111148/222208 |
0.1867 |
| 219 | 1 |
112187/224256 |
0.2492 |
| 224 | 1 |
114861/229376 |
0.7224 |
| 225 | 1 |
115213/230400 |
0.0542 |
| 227 | 2 |
232680/464896 |
0.6805 |
| 229 | 1 |
117253/234496 |
0.0207 |
| 232 | 1 |
118732/237568 |
0.2134 |
| 235 | 2 |
240535/481280 |
0.3027 |
| 236 | 1 |
120846/241664 |
0.0570 |
| 237 | 1 |
121032/242688 |
1.2667 |
| 238 | 1 |
121802/243712 |
0.2188 |
| 240 | 1 |
122412/245760 |
1.8881 |
| 241 | 1 |
123381/246784 |
0.0443 |
| 245 | 1 |
125995/250880 |
2.2161 |
| 250 | 1 |
128051/256000 |
0.2016 |
| 251 | 1 |
128793/257024 |
1.1085 |
| 252 | 2 |
258266/516096 |
0.6069 |
| 259 | 1 |
132992/265216 |
1.4913 |
| 272 | 1 |
139725/278528 |
1.7470 |
| 278 | 1 |
142232/284672 |
0.3898 |
| 280 | 1 |
143009/286720 |
1.3110 |
| 282 | 1 |
144776/288768 |
1.4590 |
| 284 | 1 |
145732/290816 |
1.2016 |
| 286 | 1 |
146644/292864 |
0.7835 |
| 291 | 1 |
149196/297984 |
0.7474 |
| 292 | 1 |
150030/299008 |
1.9239 |
| 296 | 1 |
151540/303104 |
0.0436 |
| 305 | 1 |
155684/312320 |
1.7035 |
| 306 | 1 |
155855/313344 |
2.9190 |
| 307 | 1 |
156831/314368 |
1.2592 |
| 313 | 1 |
160538/320512 |
0.9962 |
| 315 | 1 |
160439/322560 |
2.9616 |
| 330 | 1 |
169191/337920 |
0.7948 |
| 332 | 1 |
169748/339968 |
0.8095 |
| 342 | 1 |
175610/350208 |
1.7101 |
| 343 | 1 |
175927/351232 |
1.0495 |
| 346 | 1 |
177270/354304 |
0.3965 |
| 348 | 1 |
178012/356352 |
0.5495 |
| 349 | 1 |
178566/357376 |
0.4082 |
| 357 | 1 |
182946/365568 |
0.5359 |
| 368 | 1 |
188552/376832 |
0.4431 |
| 371 | 1 |
189782/379904 |
0.5516 |
| 375 | 1 |
192355/384000 |
1.1458 |
| 381 | 1 |
195222/390144 |
0.4803 |
| 383 | 1 |
196677/392192 |
1.8555 |
| 387 | 1 |
197695/396288 |
1.4265 |
| 401 | 2 |
411195/821248 |
1.2602 |
| 404 | 1 |
206995/413696 |
0.4571 |
| 414 | 1 |
212109/423936 |
0.4331 |
| 423 | 1 |
216977/433152 |
1.2186 |
| 425 | 1 |
217540/435200 |
0.1819 |
| 432 | 1 |
221882/442368 |
2.0989 |
| 435 | 1 |
222783/445440 |
0.1888 |
| 438 | 1 |
223835/448512 |
1.2573 |
| 440 | 1 |
225551/450560 |
0.8075 |
| 445 | 1 |
228040/455680 |
0.5926 |
| 456 | 1 |
233269/466944 |
0.5941 |
| 465 | 1 |
238314/476160 |
0.6782 |
| 467 | 1 |
239186/478208 |
0.2372 |
| 477 | 1 |
244153/488448 |
0.2032 |
| 483 | 1 |
248038/494592 |
2.1101 |
| 500 | 2 |
512273/1024000 |
0.5396 |
| 504 | 1 |
258187/516096 |
0.3870 |
| 508 | 1 |
260856/520192 |
2.1075 |
| 525 | 1 |
269535/537600 |
2.0049 |
| 527 | 1 |
270066/539648 |
0.6589 |
| 531 | 1 |
271399/543744 |
1.2829 |
| 539 | 1 |
275737/551936 |
0.6219 |
| 555 | 1 |
283962/568320 |
0.5253 |
| 559 | 1 |
286180/572416 |
0.0740 |
| 579 | 1 |
296000/592896 |
1.1636 |
| 618 | 2 |
633017/1265664 |
0.3289 |
| 622 | 1 |
319329/636928 |
2.1677 |
| 657 | 1 |
337081/672768 |
1.6995 |
| 659 | 1 |
337721/674816 |
0.7620 |
| 666 | 1 |
341240/681984 |
0.6006 |
| 670 | 1 |
343489/686080 |
1.0841 |
| 698 | 1 |
357541/714752 |
0.3903 |
| 708 | 1 |
362383/724992 |
0.2654 |
| 724 | 1 |
371383/741376 |
1.6143 |
| 748 | 1 |
383207/765952 |
0.5279 |
| 765 | 1 |
390911/783360 |
1.7377 |
| 787 | 1 |
402579/805888 |
0.8132 |
| 791 | 1 |
404683/809984 |
0.6867 |
| 847 | 1 |
434412/867328 |
1.6063 |
| 864 | 1 |
442760/884736 |
0.8335 |
| 902 | 1 |
461910/923648 |
0.1790 |
| 973 | 1 |
498360/996352 |
0.3687 |
| 992 | 1 |
507591/1015808 |
0.6211 |
| 1005 | 1 |
514573/1029120 |
0.0256 |
| 1024 | 1 |
523462/1048576 |
1.6133 |
| 1027 | 1 |
525719/1051648 |
0.2048 |
| 1101 | 1 |
563674/1127424 |
0.0716 |
| 1241 | 1 |
635247/1270784 |
0.2573 |
| 1261 | 1 |
645933/1291264 |
0.5298 |
| 1349 | 1 |
690715/1381376 |
0.0459 |
| 1407 | 1 |
719699/1440768 |
1.1414 |
| 1415 | 1 |
724351/1448960 |
0.2143 |
| 1458 | 1 |
746586/1492992 |
0.1473 |
| 1481 | 1 |
758020/1516544 |
0.4093 |
| 1652 | 1 |
846016/1691648 |
0.2952 |
| 1742 | 1 |
891790/1783808 |
0.1707 |
| 1769 | 1 |
906121/1811456 |
0.5840 |
| 1947 | 1 |
996742/1993728 |
0.1728 |
| 2000 | 1 |
1024947/2048000 |
1.3235 |
| 2198 | 1 |
1126814/2250752 |
1.9170 |
| 2257 | 1 |
1156265/2311168 |
0.8959 |
| 2296 | 1 |
1174949/2351104 |
0.7865 |
| 2591 | 1 |
1327380/2653184 |
0.9675 |
| 4210 | 1 |
2154581/4311040 |
0.9045 |
| 4223 | 1 |
2161820/4324352 |
0.3424 |
| 4261 | 1 |
2181516/4363264 |
0.1111 |
| 4601 | 1 |
2355712/4711424 |
0.0000 |
| 4731 | 1 |
2422549/4844544 |
0.2517 |
| 5250 | 1 |
2689581/5376000 |
1.3637 |
| 5724 | 1 |
2929525/5861376 |
0.9607 |
| 6371 | 1 |
3259087/6523904 |
2.2434 |
| 6565 | 1 |
3361825/6722560 |
0.4204 |
| 8301 | 1 |
4250664/8500224 |
0.3787 |
| 12514 | 1 |
6406215/12814336 |
0.5324 |
| 12950 | 1 |
6631971/13260800 |
0.8628 |
Results by Visual Feedback Program
| Feedback Program | Runs | Hits/Tries | z |
|---|
| bellcurve | 176229 |
90230348/180458496 |
0.1638 |
| clockface | 69810 |
35741530/71485440 |
0.2815 |
| experiment | 887 |
453521/908288 |
1.3074 |
| pendulum | 98137 |
50248081/100492288 |
0.3864 |
The table at the right shows results obtained by all subjects, sorted
by the visual feedback program they selected.
Results by Goal
| Goal | Runs | Hits/Tries | z |
|---|
| 0 | 83217 |
42607108/85214208 |
0.0009 |
| 1 | 261840 |
134063355/268124160 |
0.1557 |
Each visual feedback program allows the user to choose a goal
which corresponds to either an excess of zero or one bits in
the data stream. The following table gives results by goal,
indicating how many times each goal was chosen. The default
goal is an excess of one bits.
