|
|
More seems to come out of these equations than goes in. For why otherwise would wise men invest time and energy in them?—Lewis Carroll Epstein, in Relativity Visualized
When you first start keeping your log, the very first day, enter your
weight in the “Trend” column as well as the “Weight” column.
Thereafter, calculate the number for the “Trend” column as follows:
For example, here's a log for November 1990, You're about to make the entry for November 4th. You've just weighed yourself at 171.5, and entered that number in the weight column. Your log now looks like this:
November 1990
Date Day Weight Trend Rung
---- --- ------ ----- ----
173.6
1 Thu 172.5 173.5 1
2 Fri 171.5 173.3 1
3 Sat 172 173.2 1
4 Sun 171.5 _____ 1
5 ___ ______ _____ ___
6 ___ ______ _____ ___
To compute the trend number, subtract yesterday's trend number (173.2) from today's weight (171.5):
| 171.5 |
| − 173.2 |
| −1.7 |
Next, shift the decimal point in the difference one position to the left, giving −0.17. This number is rounded to one decimal place by looking at its second decimal place and adding one to the first decimal if it's five or more. Since the second decimal place is 7, we round the number to −0.2. Finally, this number is added to yesterday's trend number (173.2). Since we're adding a negative number, the result is less:
| 173.2 |
| + −0.2 |
| 173.0 |
This result, 173.0, is entered as the trend number for the 4th.
When you begin a new log sheet for the next month, copy the trend number for the last day of the previous month to the line right below the “Trend” column heading of the new log. When you compute the trend for the first day of the new month, use that entry as the previous day's trend number.
This may seem a lot of trouble at first, but once you get accustomed to it, you can calculate the new trend number in a few seconds.
(Those conversant with mathematics will recognise this as an “exponentially smoothed moving average with 10% smoothing,” and the instructions above as the wordy equivalent of the expression Tn=Tn−1+0.1(Wn−Tn−1) where Tn is the trend number for day n and Wn is the weight number for day n. If you're using a calculator to compute the trend, use this formula. Complete mathematical definitions of various forms of moving averages are given below. The trick of avoiding division by choosing a smoothing percentage of 10% and shifting the decimal place instead has been used for decades by financial analysts making stock and commodity price charts.)
To calculate the number of pounds you're losing (or gaining) per week in a given month, subtract the final trend number for the month from the initial trend number, then divide by 4 to get weekly weight loss (or gain). For example, if on the first of the month the trend entry was 167 and on the last day of the month it stood at 160, you lost a total of 7 pounds that month. The loss per week is then 7/4, or 1.75 pounds.
To calculate the average daily calorie shortfall (or excess) for a month, take the total weight loss (or gain) that month (for example 167 − 160 = 7 pounds) measured from the trend numbers, multiply by 3500 to obtain the total calories burned from fat (or stored there), then divide by the number of days in the month (31 for July, for example) to give the average daily calorie shortfall or excess. If you started July with the trend at 167 and ended it with the trend at 160, then each day you ate an average of
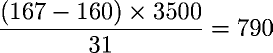
fewer calories than you burned.
It only takes a couple of minutes to make a monthly weight chart from a completed log page. It's up to you whether to update the chart every day or wait 'till the end of the month and plot all the data in one sitting. One advantage of making the chart monthly is that at the end of the month you know the weight range for the month so you don't have problems with a line running off the bottom (or, horror of horrors, the top) of the page.
To make a chart, get a piece of graph paper and draw axes at the bottom, left, and right. Mark off ticks on the bottom for every day, and ticks at the left for pounds. The right axis runs from 0 to 48 and is used to plot the rung in the exercise program you completed each day. To save time, make up a blank chart with the axes drawn in, the days of the month marked on the horizontal axis, and the rung numbers on the right, then run off a year's supply on a copier. All you have to do each month is label the weight scale on the vertical axis and plot the data. Plot both the daily weight readings and trend data on the chart, along with the exercise rung. The best way to distinguish the different lines on the chart is to draw them in different colours, for example black for daily weight, blue for the trend line, and red for the exercise rung line. Using all those different coloured pens may make you feel like a nerd, but since you aren't using a computer, it's OK. Model your hand-drawn charts after the computer-generated ones.
To calculate how long it will take to reach a weight goal starting from a given weight, on a diet that restricts the calories you eat to some number fewer than you burn every day, first subtract the weight goal from the starting weight to get the number of pounds you need to lose. Multiplying by 3500 obtains the total number of calories you need to burn from fat to reduce your weight by the desired amount. Now divide by the daily calorie shortfall anticipated in your diet plan. The result will be the number of days it should take to lose the weight. You can divide the number of days by 7 to get weeks, or by 30 for time in months.
Using the numbers from the diet planning example, we calculate as follows. Subtracting the weight, 145, from the initial weight, 215, gives a weight loss of 70 pounds. Multiplying this by 3500 calories/pound indicates that a total of 245000 calories of fat (whew!) will have to be burned to lose that 70 pounds. The dieter intends to reduce his daily intake by 862 calories below what he burns, so dividing this into 245000 tells us how long the diet will take: 284 days. Dividing by 7 expresses this as 41 weeks (after rounding to the nearest week); dividing by 30 gives the duration as slightly less than 9 1/2 months.
To calculate the extra minutes per day equivalent to extending your life by a given number of years, start with a guess at your minimum lifespan, overweight and out of shape. If you're less than 60, use 65 years, figuring on dropping dead on the day you retire. Life's like that, isn't it? If you're 60 or above, add 10 years to your current age. Next, subtract your age from this number, giving the years you'd live in your present shape. For example, if you're 40 now, and assuming you'd live to 65 without losing weight or exercising, you'd calculate 65 − 40 = 25 years to live.
Next, make an assumption about the number of years you'll increase your life expectancy by exercising. The figure of 3 years used in the life extension example is conservative; some estimates run as high as 4 years reduced expectancy simply from being 15 pounds overweight. Multiply the years of increased lifespan by 1440, the number of minutes in a day (24 × 60 = 1440), to obtain the total minutes of increased lifespan, then divide by the number of years you'd live otherwise to obtain the extra minutes per day. Assuming 3 years of increased life span and 25 years to live otherwise, you'd calculate:
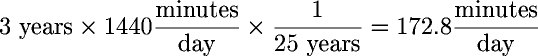
Thus, if losing weight and exercising extends your life by 3 years past age 65, you've added extra time to your life equivalent to more than 172 minutes a day: almost three extra hours!
But at what cost in time? If you extend your life 3 years past age 65 with 15 minutes of daily exercise, you have a net gain of 172 − 15 = 157 minutes a day, still more than two and a half hours. Another perspective on the time invested in a longer life is given by calculating the total years you'll spend exercising from now until the end of your estimated lifespan. Take your estimated years to live, multiply by the minutes per day spent exercising, and divide by 1440. Using the same assumptions as before, and figuring on 15 minutes a day of exercise, yields:
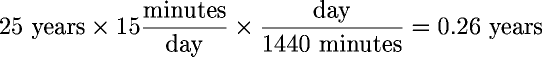
Thus, in the 25 years from age 40 to 65, you'd spend a total of about a quarter of a year exercising. If that bought you three more years to live, you'd end up with 2 3/4 extra years, more than 1000 additional days (2.75 × 365 ≈ 1000), to enjoy life, even if you figure the time spent on exercise was otherwise completely wasted and you derived no other benefits from it apart from a longer life span.
The thermostat feedback system modeled by the Excel workspace FEEDLAB.XLS isn't really practical to work by hand. The amount of calculation required to simulate one day is such that you'll almost certainly give up before gaining the intuitive understanding of feedback that comes from changing parameters and seeing the computer immediately simulate the consequences.
Nonetheless, here is the mathematical basis of the model. From these equations you can implement the simulation in another spreadsheet or as a standalone program. The parameters that control the model are identified by their labels on the FEEDLAB control panel.
Given:
| A | = | Range |
| D | = | Delay |
| G | = | Goal |
| L | = | Insulation |
| N | = | Noise |
| P | = | Power |
| R | = | Random |
Calculate the following variables for each time step i:
| Oi | = | Outside temperature |
| Ei | = | Error (deviation from goal) |
| Ci | = | Correction applied by feedback |
| Ti | = | Inside temperature |
with the following initial conditions:
| O0 | = | 70 |
| T0 | = | 70 |
For each 10 minute time interval
![]() calculate the inside temperature Ti as follows.
calculate the inside temperature Ti as follows.
![]() is a pseudorandom number ranging from −1 to 1, with a new value
generated at each occurrence of
is a pseudorandom number ranging from −1 to 1, with a new value
generated at each occurrence of
![]() .
.

Quick and easy instructions for calculating the daily trend from weight are given above. That calculation uses a particular exponentially smoothed moving average chosen for ease of calculation as well its effectiveness in extracting the trend from daily weights. This section presents the mathematical definition of all the forms of moving averages described in the Signal and Noise chapter. You don't have to understand this material to understand moving averages, and it's certainly not necessary to use moving averages to control your weight. If you're interested in experimenting on your own with moving averages on a computer, these equations provide the foundation for the programs you'll write.
All moving averages operate on a time series of measurements, M1, M2,…, Md, where d is the total number of measurements made to date and Md is the most recently made measurement. For convenience in the discussion, we'll assume one measurement is made per day; any other regular interval is equivalent.
The n day simple moving average for day d is computed by:
If we have ten measurements, M1 through M10, and we wish to compute a four day moving average, the moving averages for successive days are:
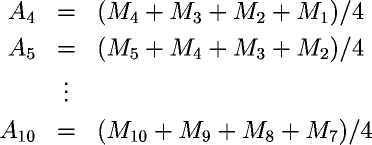
We can't compute a four day moving average until we have four days worth of data. That's why the first moving average in this example is A4.
A weighted moving average is calculated by defining weight factors, W1, W2,… Wn, for each day in the n day moving average. The weighted moving average for day d is then:
Note that if all the weights, Wi are 1, this equation reduces to that of a simple moving average.
An exponentially smoothed moving average is a weighted moving average in which the weight factors are powers of S, the smoothing constant. An exponentially smoothed moving average is computed over all the data accumulated so far instead of being chopped off after some number of days. For day d the exponentially smoothed moving average is:
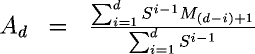
But this is just a geometric sequence! The next term in such a sequence is given by: Ad=(1−S)Md+SAd−1. Calculation is expedited and comprehension served if we substitute: P=1−S for S into the equation for the next term. Doing a little algebra, we discover:
![A[d] = A[d - 1] + P (M[d] - A[d - 1])](figures/pencil8.png)
This reformulation makes the operation of smoothing very intuitive. Every day, we take the old trend number Ad−1, calculate the difference between it and today's measurement Md, then add a percentage of that difference P to the old trend value obtain the new one. Obviously, the closer P is to 1 (and hence the closer S is to zero), the more influence the new measurement has upon the trend. If P=1, the old trend value Ad−1 cancels out and the moving average tracks the data precisely.
For example, with the smoothing constant S = 0.9 we use on weight data, we calculate the new trend value Ad from the previous trend value Ad−1 and today's weight Md as:
![A[d] = A[d - 1] + 0.1 (M[d] - A[d - 1])](figures/pencil9.png)
In discussions of exponentially smoothed moving averages, particularly their financial applications, beware of confusing the smoothing constant S with the variant form P = 1 − S introduced to simplify calculation and make the effect of the new data on the moving average more apparent. P is often referred to as the “smoothing percentage”; the term “10% smoothing” refers to a calculation in which P = 10 / 100 = 0.1 and hence S = 0.9.
To calculate the rate of weight loss or gain and the calorie shortfall or excess responsible for it from the moving average trend line, the Excel spreadsheet finds the straight line trend that best fits the curve traced out by the moving average by the method of least squares. The process of finding a line that accurately represents the trend of a collection of data points is called linear regression, and the least squares method is the most frequently used approach to the problem.
Any non-vertical straight line (you'd be in a fine pickle if your weight trend line were vertical, wouldn't you?) can be expressed in the form:
Y = mX + b
where m is the slope, giving the change in the Y axis value for each unit change along the X axis, and b is the intercept, the point at which the line crosses the Y axis when X is zero.
To find m and b for the line that best fits a collection of data points D1, D2, … Dn we calculate:
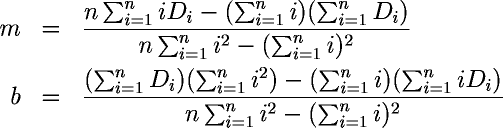
Since we're only interested in the rate of change, we only need the slope, m, which gives the daily rate of change in the line that best fits the moving average trend curve. From the slope, the average weight change per week is just seven times the daily change,
7m
and the average daily calorie deficit (if negative) or excess (if positive) is:
3500m
|
|